如图，在三棱锥 $A - BCD$ 中，$\angle BCD = 90^\circ $，$BC = CD = AB = 1$，$AB \perp BCD$，$E$ 为 $AC$ 中点，$F$ 在线段 $AD$ 上，且 $\dfrac{{AF}}{{AD}} = \lambda $．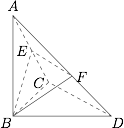
【难度】
【出处】
2008年西北工业大学自主招生测试
【标注】
-
当 $\lambda $ 为何值时，$BEF$ $ \perp ACB$，并证明；标注答案$\dfrac 12$解析易知$$CD \perp BC, CD \perp AB,$$所以$$CD \perp ABC,$$于是只需 $EF\parallel CD$ 即可，故 $\lambda = \dfrac{1}{2}$．
-
在 $(1)$ 的条件下，求二面角 $E - CF - B$ 的大小．标注答案$60^\circ $解析由 $(1)$ 知 $EF \perp BE$，又 $BE \perp AC$，所以$$BE \perp ECF.$$作 $EH \perp CF$ 于 $H$，则 $\angle EHB$ 为所求二面角的平面角，如图．
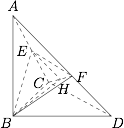在 $\mathrm{Rt}\triangle ACD$ 中，$$AC = \sqrt 2 , CD = 1, AD = \sqrt 3 ,$$于是$$EF = \dfrac{1}{2}, EC = \dfrac{{\sqrt 2 }}{2}, CF = \dfrac{{\sqrt 3 }}{2},$$从而在 $\mathrm{Rt}\triangle ECF$ 中，$EH = \dfrac{{\sqrt 6 }}{6}$，
故$$\tan \angle EHB = \dfrac{{BE}}{{EH}} = \sqrt 3 ,$$二面角 $E - CF - B$ 的大小为 $60^\circ $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
