查看数据源：59128ce7e020e7000a798bc7
一个平面，由红点和蓝点组成，而且既有红点也有蓝点．对于给定的任意长度 $a$（$a > 0$），证明：
【难度】
【出处】
2008年中国科学技术大学自主招生保送生测试
【标注】
  • 知识点
    >
    组合数学
    >
    抽屉原理
  • 题型
    >
    组合数学
    >
    组合证明
  • 方法
    >
    论述方式
    >
    反证法
  • 题型
    >
    组合数学
    >
    组合证明
  1. 平面内存在两个同色点，距离为 $a$；
    标注
    • 知识点
      >
      组合数学
      >
      抽屉原理
    • 题型
      >
      组合数学
      >
      组合证明
    答案
    略
    解析
    取一个边长为 $a$ 的正三角形，由抽屉原理，即证明了命题．
  2. 存在两个异色点，距离为 $a$．
    标注
    • 方法
      >
      论述方式
      >
      反证法
    • 题型
      >
      组合数学
      >
      组合证明
    答案
    略
    解析
    设平面上 $R$ 为红点，$B$ 为蓝点，那么一定可以用若干条长度为 $a$ 的线段将 $R$ 与 $B$ 连接起来．
    如图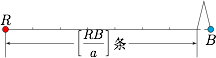，用反证法．
    如果所有这些长度为 $a$ 的线段端点均为同色，那么所有端点均同色，矛盾．
    于是必然存在一条长度为 $a$ 的线段，其端点异色，这就证明了 $(2)$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.250131s