题目 设 $f\left( x \right) = {x^2} + \left( {k + 1} \right)x + 2k + 1$，$g\left( k \right)$ 是 $k$ 的多项式． 问题1 设 $f\left( a \right)$ 与 $k$ 无关，求常数 $a$； 答案1 $-2$ 解析1 $f\left( x \right) = k\left( {x + 2} \right) + {x^2} + x + 1$，所以 $f\left( { - 2} \right)$ 与 $k$ 无关，$a = - 2$； 备注1 问题2 求一次多项式 $g\left( k \right)$，使得 $f\left( {g\left( k \right)} \right)$ 与 $k$ 无关； 答案2 $g(k)=-k+1$ 解析2 设 $g\left( k \right) = ak + b$，$a \ne 0$，则$$f\left( {g\left( k \right)} \right) = \left( {{a^2} + a} \right){k^2} + \left( {2ab + a + b + 2} \right)k + {b^2} + b + 1.$$该多项式与 $k$ 无关，所以$$\begin{cases}{a^2} + a = 0,\\ 2ab + a + b + 2 = 0.\end{cases}$$解得 $\begin{cases} a = - 1,\\ b=1.\end{cases}$ 所以$$g(k)=-k+1.$$ 备注2 问题3 设 $g\left( k \right)$ 是二次以上多项式，证明 $f\left( {g\left( k \right)} \right)$ 必与 $k$ 有关； 答案3 略 解析3 设 $g\left( k \right)$ 的最高项为 ${a_n}{k^n}$，${a_n} \ne 0$，$n \geqslant 3$，则 $f\left( {g\left( k \right)} \right)$ 的最高项为 ${a_n}^2 \cdot {k^{2n}}$，而 $a_n^2 \ne 0$，所以 $f\left( {g\left( k \right)} \right)$ 必与 $k$ 有关． 备注3 问题4 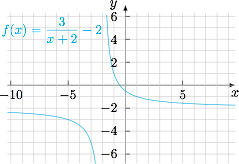设 $\alpha,\beta $ 为 $f\left( x \right) = 0$ 的解，试求 $\alpha ,\beta $ 满足的方程，并用图形表示出来，其中 $\alpha $ 取作横坐标轴，$\beta $ 取作纵坐标轴； 答案4 $\beta = \dfrac{3}{{\alpha + 2}} - 2$ 解析4 由韦达定理，$$\begin{cases}\alpha + \beta = - \left( {k + 1} \right), \\ \alpha \beta = 2k + 1,\end{cases}$$消参有 $\left( {\alpha + 2} \right)\left( {\beta + 2} \right) = 3$．于是 $\beta = \dfrac{3}{{\alpha + 2}} - 2$，图象为双曲线，如图所示．<img src="/static/images/ba7c1f056e40f0c42e70b691025b9f66.png" class="img-responsive" /> 备注4 问题5 在 $(4)$ 中，如果 $\alpha ,\beta $ 是整数，求出这样的 $\alpha ,\beta $ 对应的所有的 $k$ 值． 答案5 $-1$ 或 $7$ 解析5 因为 $\left( {\alpha + 2} \right)\left( {\beta + 2} \right) = 3$，所以 $(\alpha +2,\beta+2)=(3,1)$ 或 $(1,3)$ 或 $(-1,-3)$ 或 $(-3,-1)$．<br/>解得 $(\alpha,\beta)=(1,-1)$，$(-1,1)$，$(-3,-5)$，$(-5,-3)$．<br/>所以 $k$ 的值为 $-1$ 或 $7$． 备注5