如图，在正三棱锥 $P - ABC$ 中，侧棱长为 $3$，底面边长为 $2$，$E$ 为 $BC$ 的中点，$EF \perp PA$ 于 $F$．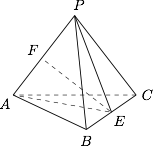
【难度】
【出处】
2009年华南理工大学自主招生保送生选拔考试
【标注】
-
求证：$EF$ 为异面直线 $PA$ 与 $BC$ 的公垂线；标注答案略解析由于 $P - ABC$ 是正三棱锥，$E$ 是 $BC$ 的中点，
所以 $AE \perp BC$，$PE \perp BC$．
于是 $BC \perp $ 平面 $APE$，而 $EF$ 在平面 $APE$ 内，因此 $EF \perp BC$．
又 $EF \perp PA$，所以 $EF$ 为 $PA$ 与 $BC$ 的公垂线段． -
求异面直线 $PA$ 与 $BC$ 的距离；标注答案$\dfrac{{\sqrt {23} }}{3}$解析由 $(1)$ 知 $EF$ 即异面直线 $PA$ 与 $BC$ 的距离．在 $\triangle PAE$ 中作 $PQ\perp AE$ 于点 $Q$，如图：
则 $PQ = \sqrt {P{A^2} - A{Q^2}} = \dfrac{{\sqrt {69} }}{3}$．对 $\triangle APE$，有$$EF = \dfrac{{AE \cdot PQ}}{{AP}} = \dfrac{{\sqrt 3 \cdot \dfrac{{\sqrt {69} }}{3}}}{3} = \dfrac{{\sqrt {23} }}{3}.$$所以，异面直线 $PA$ 与 $BC$ 的距离为 $\dfrac{{\sqrt {23} }}{3}$． -
求点 $B$ 到面 $APC$ 的距离．标注答案$\dfrac{{\sqrt {46} }}{4}$解析用等体积法．$$d\left( {B, APC} \right) = \dfrac{{{S_{\triangle ABC}}}}{{{S_{\triangle APC}}}} \cdot d\left( {P,ABC} \right) = \dfrac{{\sqrt 3 }}{{1 \cdot \sqrt {{3^2} - {1^2}} }} \cdot \dfrac{{\sqrt {69} }}{3} = \dfrac{{\sqrt {46} }}{4}.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
