如图,抛物线与 $x$ 轴交于点 $A\left(-5,0\right)$,和点 $B\left(3,0\right)$,与 $y$ 轴交于点 $C\left(0,5\right)$.有一宽度为 $1$,长度足够的矩形(阴影部分)沿 $x$ 轴方向平移,与 $y$ 轴平行的一组对边交抛物线于点 $P$ 和 $Q$,交直线 $AC$ 于点 $M$ 和 $N$,交 $x$ 轴于点 $E$ 和 $F$.在矩形的平移过程中,当以点 $P$,$ Q $,$ M $,$N$ 为顶点的四边形是平行四边形时,求点 $M$ 的坐标.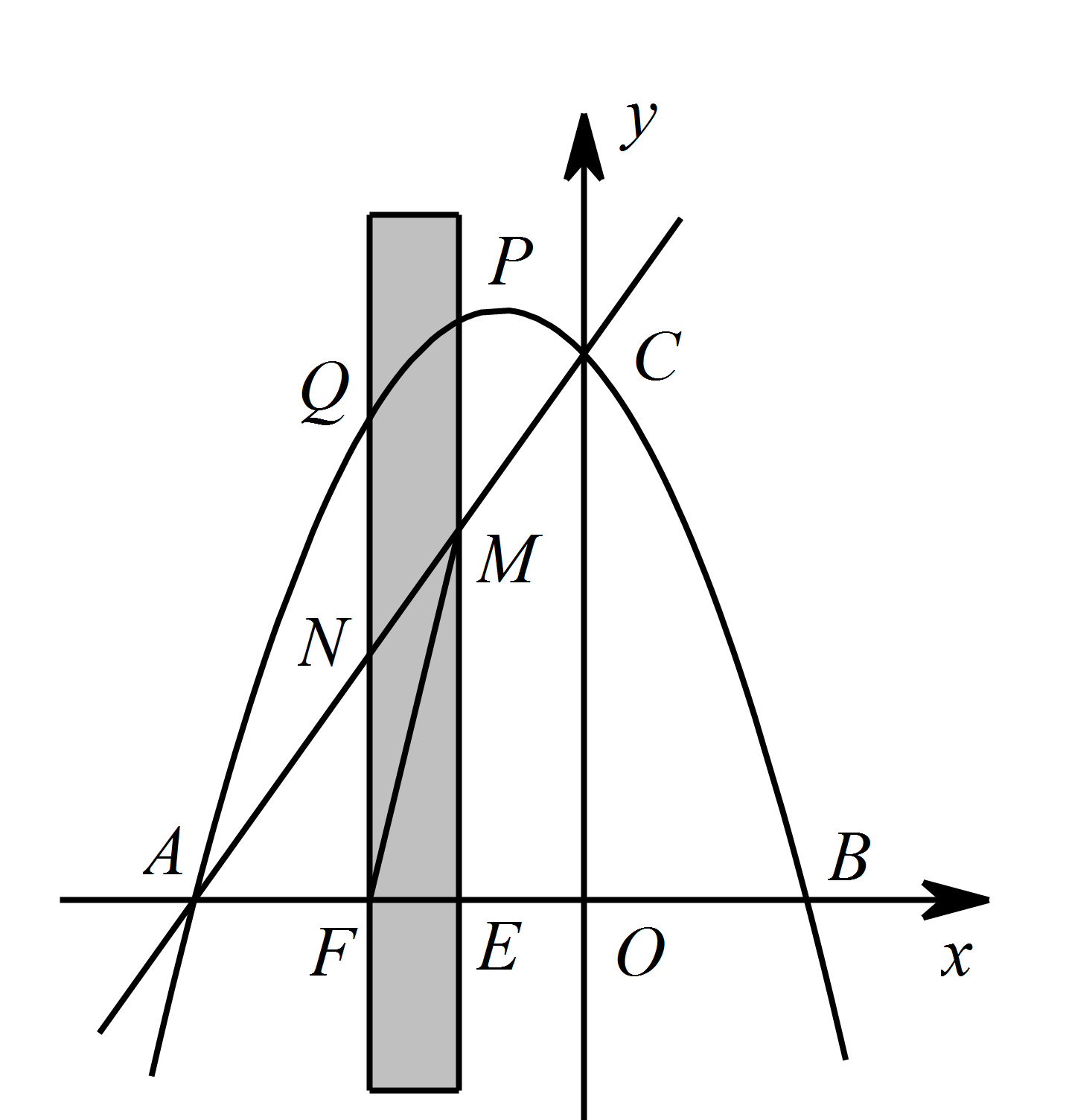

【难度】
【出处】
无
【标注】
【答案】
根据题意,$ A\left(-5,0\right) $,$ B\left(3,0\right) $ 在 $ x $ 轴上,
设抛物线为 $ y=a\left(x+5\right)\left(x-3\right) $.
$\because$ 抛物线过点 $ \left(0,5\right) $,
$\therefore$ $ a=-\dfrac13 $.
$\therefore$ 抛物线解析式为 $ y=-\dfrac13\left(x+5\right)\left(x-3\right)=-\dfrac13x^2-\dfrac23x+5 $.
设直线 $ AC $ 的解析式 $ y=kx+n $,
由题意,得 $\begin{cases}-5k+n=0,\\n=5.\end{cases}解得\begin{cases}k=1,\\n=5.\end{cases}$
$\therefore$ 直线 $ AC $ 的解析式 $ y=x+5 $.
由已知,点 $ Q $,$ N $,$ F $ 及点 $ P $,$ M $,$ E $ 横坐标分别相同.
设 $ F\left(t,0\right) $,$ E\left(t+1,0\right) $,点 $ M $,$ N $ 在直线 $ y=x+5 $ 上,
$\therefore$ $ N\left(t,t+5\right) $,$ M\left(t+1,t+6\right) $,
$\because$ 点 $ P $,$ Q $ 在抛物线 $ y=-\dfrac13x^2-\dfrac23x+5 $ 上,
$\therefore$ $ Q\left(t,-\dfrac13t^2-\dfrac23t+5\right) $,$ P\left(t+1,-\dfrac13t^2-\dfrac43t+4\right) $.
在矩形平移过程中,以 $ P $,$ Q $,$ N $,$ M $ 为顶点的平行四边形有两种情况:
① 点 $ Q $,$ P $ 在直线 $ AC $ 同侧时,$ QN=PM $.
$\therefore$ $ \left(-\dfrac13t^2-\dfrac23t+5\right)-\left(t+5\right)=\left(-\dfrac13t^2-\dfrac43t+4\right)-\left(t+6\right) $,
解得,$ t=-3 $.
$\therefore$ $ M\left(-2,3\right) $.
② 点 $ Q $,$ P $ 在直线 $ AC $ 异侧时,$ QN=MP $.
$\therefore$ $ \left(-\dfrac13t^2-\dfrac23t+5\right)-\left(t+5\right)=\left(t+6\right)-\left(-\dfrac13t^2-\dfrac43t+4\right) $,
解得,$ t_1=-3+\sqrt6 $,$ t_2=-3-\sqrt6 $,
$\therefore$ $ M\left(-2+\sqrt6,3+\sqrt6\right) $ 或 $ \left(-2-\sqrt6,3-\sqrt6\right) $.
$\therefore$ 符合条件的点 $ M $ 是 $ \left(-2,3\right) $,$ \left(-2+\sqrt6,3+\sqrt6\right) $ 或 $ \left(-2-\sqrt6,3-\sqrt6\right) $
设抛物线为 $ y=a\left(x+5\right)\left(x-3\right) $.
$\because$ 抛物线过点 $ \left(0,5\right) $,
$\therefore$ $ a=-\dfrac13 $.
$\therefore$ 抛物线解析式为 $ y=-\dfrac13\left(x+5\right)\left(x-3\right)=-\dfrac13x^2-\dfrac23x+5 $.
设直线 $ AC $ 的解析式 $ y=kx+n $,
由题意,得 $\begin{cases}-5k+n=0,\\n=5.\end{cases}解得\begin{cases}k=1,\\n=5.\end{cases}$
$\therefore$ 直线 $ AC $ 的解析式 $ y=x+5 $.
由已知,点 $ Q $,$ N $,$ F $ 及点 $ P $,$ M $,$ E $ 横坐标分别相同.
设 $ F\left(t,0\right) $,$ E\left(t+1,0\right) $,点 $ M $,$ N $ 在直线 $ y=x+5 $ 上,
$\therefore$ $ N\left(t,t+5\right) $,$ M\left(t+1,t+6\right) $,
$\because$ 点 $ P $,$ Q $ 在抛物线 $ y=-\dfrac13x^2-\dfrac23x+5 $ 上,
$\therefore$ $ Q\left(t,-\dfrac13t^2-\dfrac23t+5\right) $,$ P\left(t+1,-\dfrac13t^2-\dfrac43t+4\right) $.
在矩形平移过程中,以 $ P $,$ Q $,$ N $,$ M $ 为顶点的平行四边形有两种情况:
① 点 $ Q $,$ P $ 在直线 $ AC $ 同侧时,$ QN=PM $.
$\therefore$ $ \left(-\dfrac13t^2-\dfrac23t+5\right)-\left(t+5\right)=\left(-\dfrac13t^2-\dfrac43t+4\right)-\left(t+6\right) $,
解得,$ t=-3 $.
$\therefore$ $ M\left(-2,3\right) $.
② 点 $ Q $,$ P $ 在直线 $ AC $ 异侧时,$ QN=MP $.
$\therefore$ $ \left(-\dfrac13t^2-\dfrac23t+5\right)-\left(t+5\right)=\left(t+6\right)-\left(-\dfrac13t^2-\dfrac43t+4\right) $,
解得,$ t_1=-3+\sqrt6 $,$ t_2=-3-\sqrt6 $,
$\therefore$ $ M\left(-2+\sqrt6,3+\sqrt6\right) $ 或 $ \left(-2-\sqrt6,3-\sqrt6\right) $.
$\therefore$ 符合条件的点 $ M $ 是 $ \left(-2,3\right) $,$ \left(-2+\sqrt6,3+\sqrt6\right) $ 或 $ \left(-2-\sqrt6,3-\sqrt6\right) $
【解析】
略
答案
解析
备注