查看数据源：59cb1275778d4700085f6f55
函数 $f(x)=ax^m(1-x)^n$ 在区间 $[0,1]$ 上的图象如图所示，则 $m,n$ 的值可能是 \((\qquad)\)
A: $m=2,n=1$
B: $m=1,n=2$
C: $m=2,n=3$
D: $m=3,n=2$
【难度】
【出处】
2011年高考安徽卷（理）
【标注】
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
    >
    利用导数研究函数的极值
【答案】
BC
【解析】
解法一 函数 $f(x)$ 的导函数为$$f(x)=-a(1-x)^{n-1}x^{m-1}\left[(m+n)x-m\right],$$其极大值点$$\dfrac{m}{m+n}<\dfrac 12,$$于是 $m<n$．
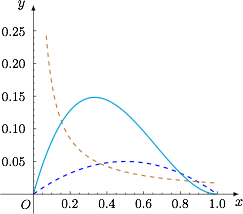解法二将 $f(x)$ 分解为两个函数的乘积：$$f(x)=ax^n(1-x)^n\cdot x^{m-n},$$前一个部分的图象关于 $x=0.5$ 对称．当 $m<n$ 时，函数 $y=x^{m-n}$ 的图象在 $x=0.5$ 两侧为左高右低，因此会引起函数图象的“重心”向左侧移动，如图．当 $m=n$ 时，函数 $f(x)$ 的图象关于 $x=0.5$ 对称，不符合题意；当 $m>n$ 时，函数 $y=x^{m-n}$ 的图象在 $x=0.5$ 两侧为左低右高，因此会引起函数图象的“重心”向右侧移动，如图．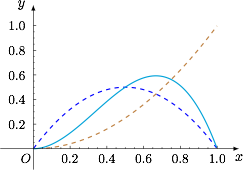
题目 答案 解析 备注
0.109963s