如图 ①，$\triangle ABC$ 与 $\triangle CDE$ 是等腰直角三角形，直角边 $AC$，$CD$ 在同一条直线上，点 $M$，$N$ 分别是斜边 $AB$，$DE$ 的中点，点 $P$ 为 $AD$ 的中点，连接 $AE$，$BD$．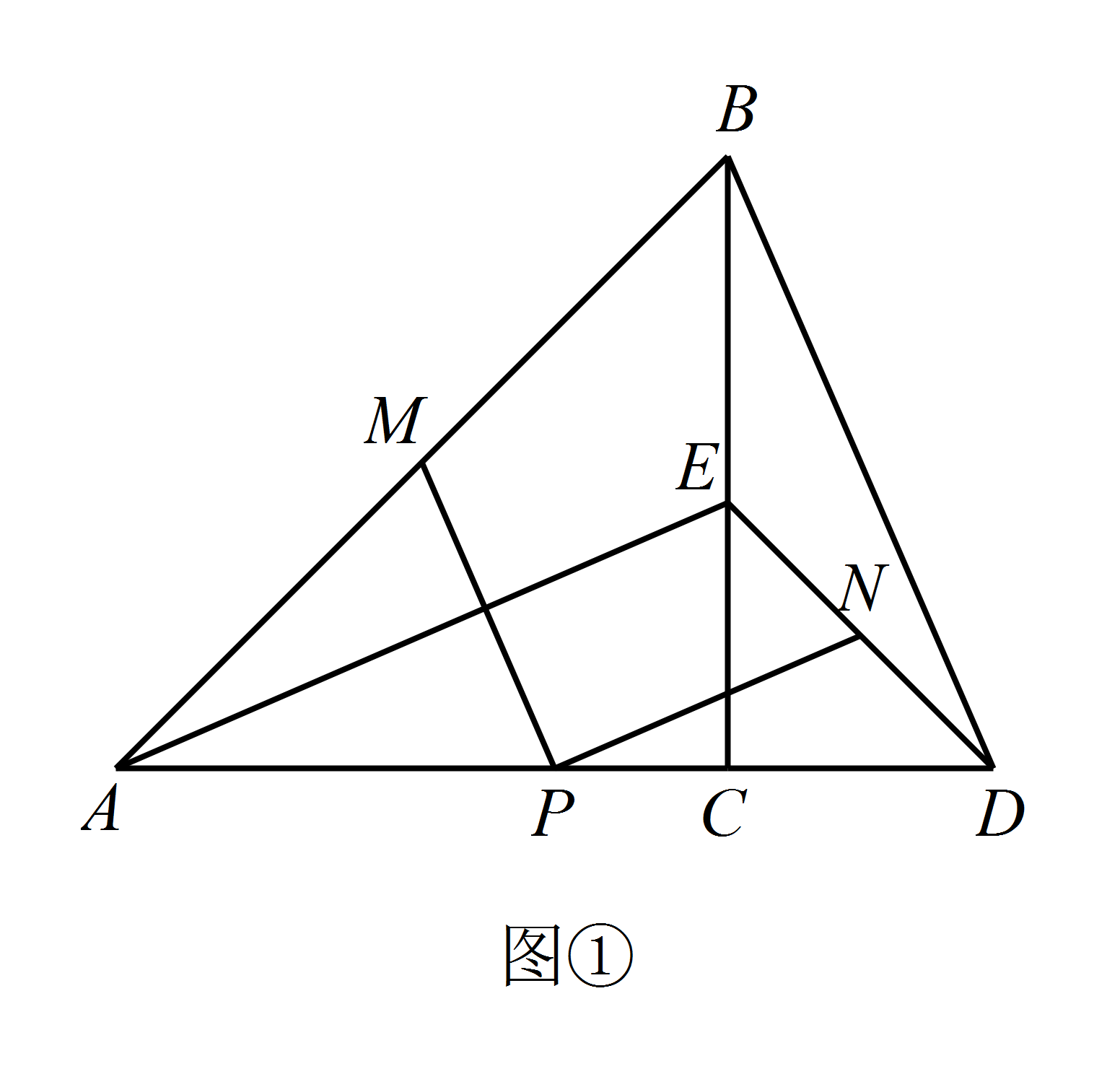
【难度】
【出处】
无
【标注】
-
猜想 $PM$ 与 $PN$ 的数量关系及位置关系，请直接写出结论；标注答案$PM= PN$，$PM\perp PN$解析略
-
现将图 ① 中的 $\triangle CDE$ 绕着点 $C$ 顺时针旋转 $ \alpha \left(0^\circ <\alpha <90^\circ\right) $，得到图 ②，$AE$ 与 $MP$，$BD$ 分别交于点 $G$，$H$．请判断 $(1)$ 中的结论是否成立？若成立，请证明；若不成立，请说明理由；
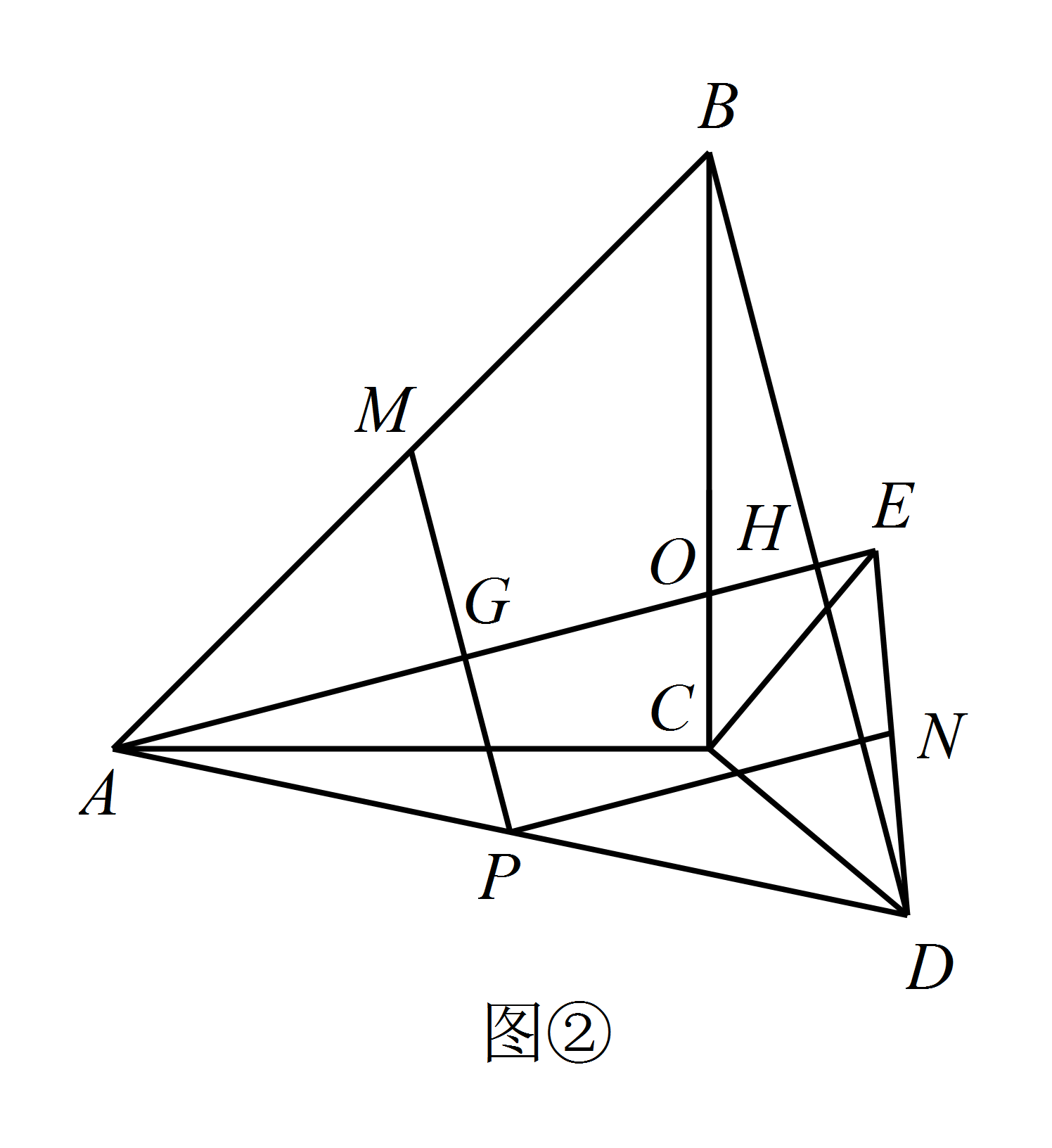标注答案成立解析因为 $\triangle ACB$ 和 $\triangle ECD$ 是等腰直角三角形，
所以 $AC=BC$，$EC=CD$，
$\angle ACB=\angle ECD=90^\circ$．
所以 $\angle ACB +\angle BCE=\angle ECD +\angle BCE$．
所以 $\angle ACE=\angle BCD$．
所以 $\triangle ACE\cong\triangle BCD$．
所以 $AE=BD$，$\angle CAE=\angle CBD$．
又因为 $\angle AOC=\angle BOE$，$\angle CAE=\angle CBD$，
所以 $\angle BHO=\angle ACO=90^\circ$．
因为点 $P,M,N$ 分别为 $AD,AB,DE$ 的中点，
所以 $PM=\dfrac12 BD$，$PM\parallel BD$；$PN=\dfrac12AE$，$PN\parallel AE$．
所以 $PM=PN$．
所以 $\angle MGE+\angle BHA=180^\circ$．
所以 $\angle MGE=90^\circ$．
所以 $\angle MPN=90^\circ$．
所以 $PM\perp PN$． -
若图 ② 中的等腰直角三角形变成直角三角形，使 $BC= kAC$，$CD= kCE$，如图 ③，写出 $PM$ 与 $PN$ 的数量关系，并加以证明．
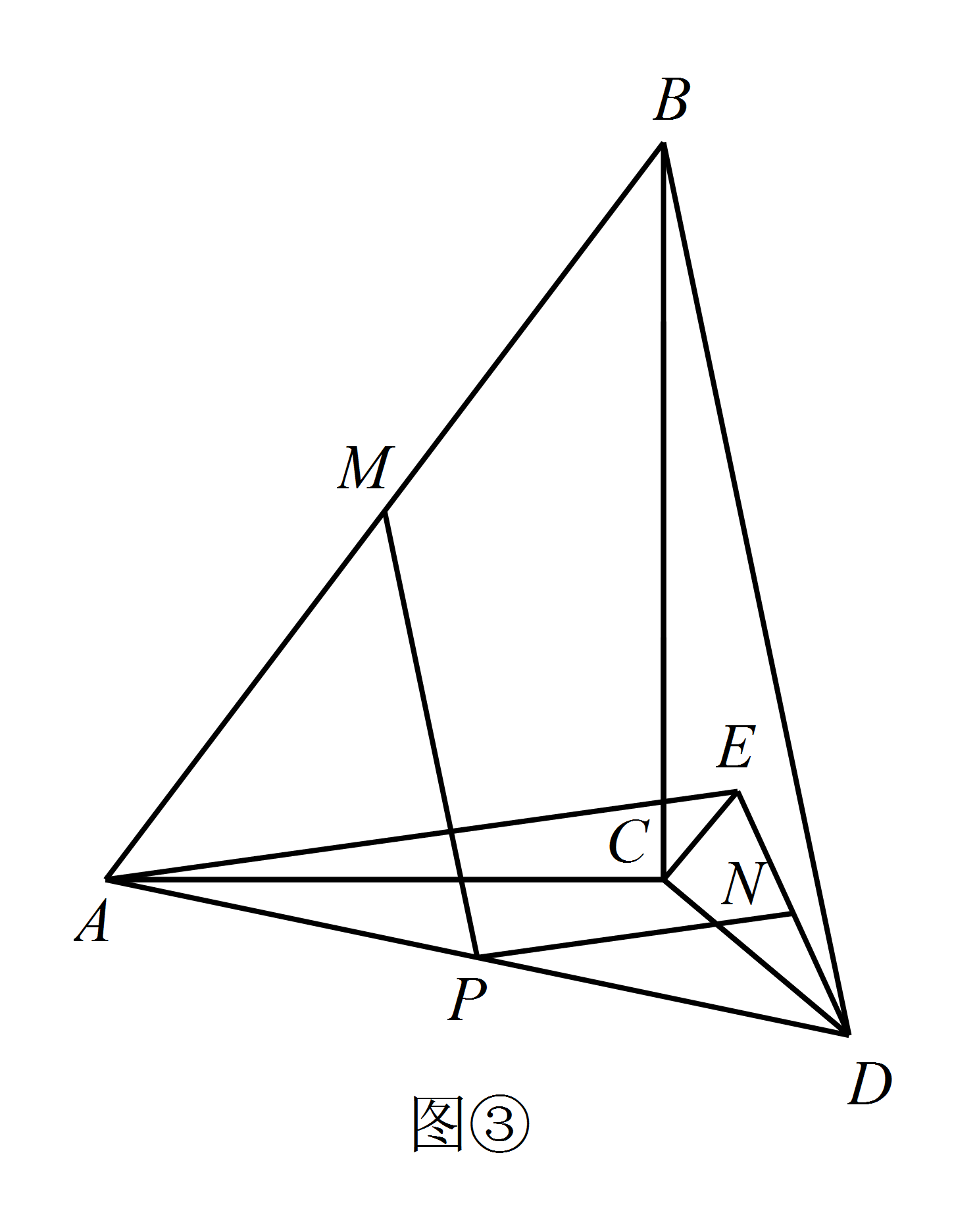标注答案$PM = kPN$解析因为 $\triangle ACB$ 和 $\triangle ECD$ 是直角三角形，
所以 $\angle ACB=\angle ECD=90^\circ$．
所以 $\angle ACB+\angle BCE=\angle ECD+\angle BCE$．
所以 $\angle ACE=\angle BCD$．
因为 $BC=kAC$，$CD=kCE$，
所以 $\dfrac{BC}{AC }=\dfrac{CD}{CE }=k$．
所以 $\triangle BCD\backsim\triangle ACE$．
所以 $BD = kAE$．
因为点 $P,M,N$ 分别为 $AD,AB,DE$ 的中点，
所以 $PM= \dfrac12BD$，$PN= \dfrac12AE$．
所以 $PM = kPN$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
