如图,已知抛物线经过原点 $O$,顶点为 $A\left(1,1\right)$,且与直线 $y=x-2$ 交于 $B$,$ C $ 两点.若点 $N$ 为 $x$ 轴上的一个动点,过点 $N$ 作 $MN\perp x$ 轴与抛物线交于点 $M$,则是否存在以 $O$,$ M $,$ N $ 为顶点的三角形与 $\triangle ABC$ 相似?若存在,请求出点 $N$ 的坐标;若不存在,请说明理由.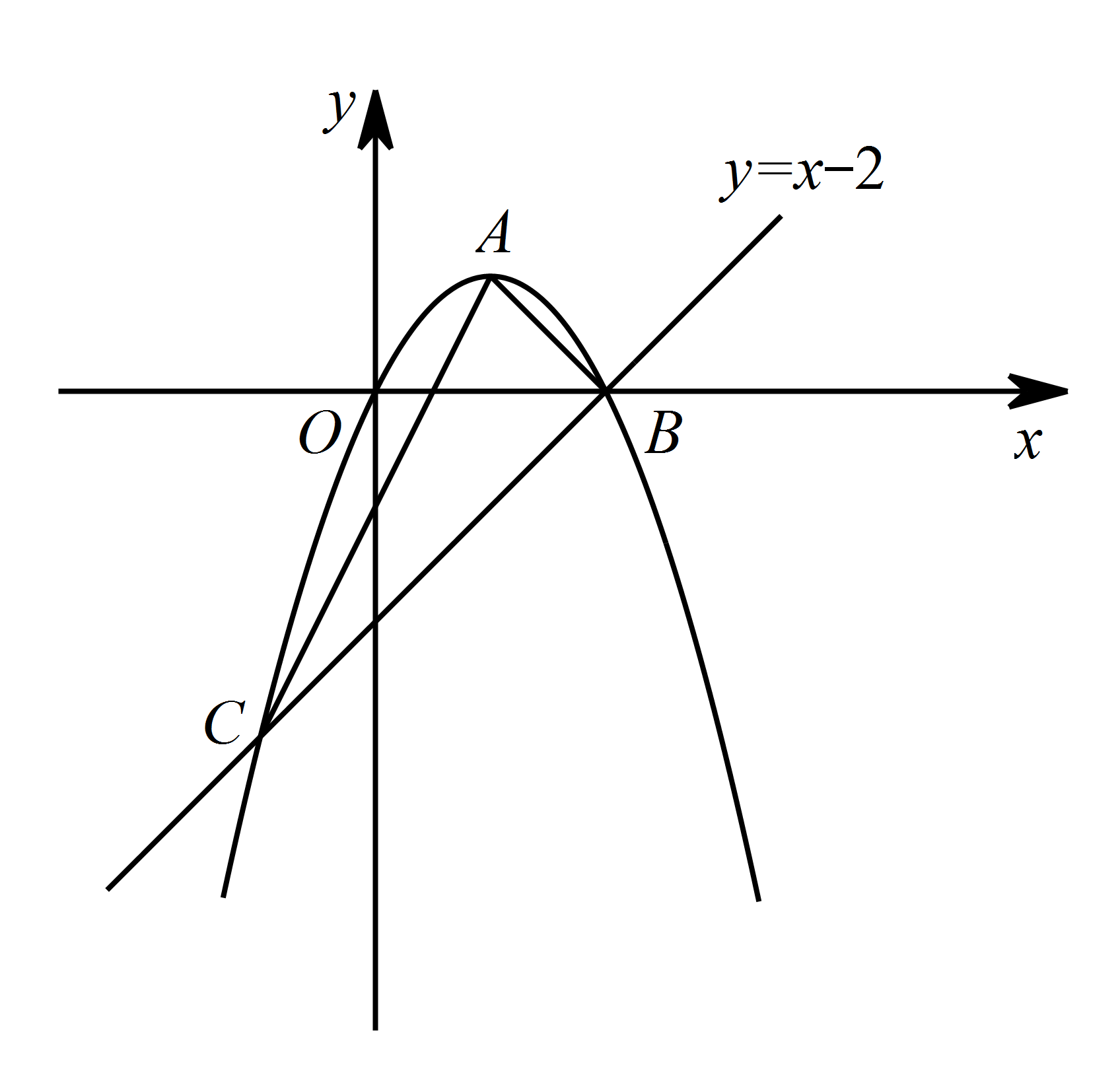

【难度】
【出处】
无
【标注】
【答案】
坐标为 $\left(\dfrac53,0\right)$ 或 $\left(\dfrac73,0\right)$ 或 $\left(-1,0\right)$ 或 $\left(5,0\right)$
【解析】
因为顶点坐标为 $\left(1,1\right)$,
所以设抛物线解析式为 $y=a\left(x-1\right)^2+1$.
又抛物线过原点,
所以 $0=a\left(0-1\right)^2+1$,解得 $a=-1$,
所以抛物线解析式为 $y=-\left(x-1\right)^2+1$.
即 $y=-x^2+2x$.
联立抛物线和直线解析式可得 $\begin{cases}-x^2+2x,\\ y=x-2.\end{cases}$
解得 $\begin{cases}x=2,\\y=0.\end{cases}$ 或 $\begin{cases}x=-1,\\y=-3.\end{cases}$
所以 $B\left(2,0\right)$,$C\left(-1,-3\right)$.
假设存在满足条件的点 $N$,设 $N\left(x,0\right)$,则 $M\left(x,-x^2+2x\right)$.
所以 $ON=\left|x\right|$,$MN=\left|-x^2+2x\right|$.
由 $(2)$ 在 $\mathrm {Rt}\triangle ABD$ 和 $\mathrm {Rt}\triangle CEB$ 中,可分别求得 $AB=\sqrt{2}$,$BC=3\sqrt{2}$.
因为 $MN\perp x$ 轴于点 $N$,
所以 $\angle ABC=\angle MNO=90^{\circ}$,
所以当 $\triangle ABC$ 和 $\triangle MNO$ 相似时,有 $\dfrac{MN}{AB }=\dfrac{ON}{ BC}$ 或 $\dfrac{MN}{ BC}=\dfrac{ON}{ AB}$.
① 当 $\dfrac{MN}{AB }=\dfrac{ON}{ BC}$ 时,则有 $\dfrac{\left|-x^2+2x\right|}{\sqrt{2} }=\dfrac{\left|x\right|}{3\sqrt{2} }$,即 $\left|x\right|\left|-x+2\right|=\dfrac13\left|x\right|$,
因为当 $x=0$ 时 $M$,$O$,$N$ 不能构成三角形,
所以 $x\ne 0$,
所以 $\left|-x+2\right|=\dfrac13$,即 $-x+2=\pm\dfrac13$,解得 $x=\dfrac53$ 或 $x=\dfrac73$,
此时 $N$ 点坐标为 $\left(\dfrac53,0\right)$ 或 $\left(\dfrac73,0\right)$;
② 当 $\dfrac{MN}{BC }=\dfrac{ON}{ AB}$ 时,则有 $\dfrac{\left|-x^2+2x\right|}{3\sqrt{2} }=\dfrac{\left|x\right|}{\sqrt{2} }$,即 $\left|x\right|\left|-x+2\right|=3\left|x\right|$,
所以 $\left|-x+2\right|=3$,即 $-x+2=\pm 3$,解得 $x=5$ 或 $x=-1$,
此时 $N$ 点坐标为 $\left(-1,0\right)$ 或 $\left(5,0\right)$,
综上可知存在满足条件的 $N$ 点,其坐标为 $\left(\dfrac53,0\right)$ 或 $\left(\dfrac73,0\right)$ 或 $\left(-1,0\right)$ 或 $\left(5,0\right)$.
所以设抛物线解析式为 $y=a\left(x-1\right)^2+1$.
又抛物线过原点,
所以 $0=a\left(0-1\right)^2+1$,解得 $a=-1$,
所以抛物线解析式为 $y=-\left(x-1\right)^2+1$.
即 $y=-x^2+2x$.
联立抛物线和直线解析式可得 $\begin{cases}-x^2+2x,\\ y=x-2.\end{cases}$
解得 $\begin{cases}x=2,\\y=0.\end{cases}$ 或 $\begin{cases}x=-1,\\y=-3.\end{cases}$
所以 $B\left(2,0\right)$,$C\left(-1,-3\right)$.
假设存在满足条件的点 $N$,设 $N\left(x,0\right)$,则 $M\left(x,-x^2+2x\right)$.
所以 $ON=\left|x\right|$,$MN=\left|-x^2+2x\right|$.
由 $(2)$ 在 $\mathrm {Rt}\triangle ABD$ 和 $\mathrm {Rt}\triangle CEB$ 中,可分别求得 $AB=\sqrt{2}$,$BC=3\sqrt{2}$.
因为 $MN\perp x$ 轴于点 $N$,
所以 $\angle ABC=\angle MNO=90^{\circ}$,
所以当 $\triangle ABC$ 和 $\triangle MNO$ 相似时,有 $\dfrac{MN}{AB }=\dfrac{ON}{ BC}$ 或 $\dfrac{MN}{ BC}=\dfrac{ON}{ AB}$.
① 当 $\dfrac{MN}{AB }=\dfrac{ON}{ BC}$ 时,则有 $\dfrac{\left|-x^2+2x\right|}{\sqrt{2} }=\dfrac{\left|x\right|}{3\sqrt{2} }$,即 $\left|x\right|\left|-x+2\right|=\dfrac13\left|x\right|$,
因为当 $x=0$ 时 $M$,$O$,$N$ 不能构成三角形,
所以 $x\ne 0$,
所以 $\left|-x+2\right|=\dfrac13$,即 $-x+2=\pm\dfrac13$,解得 $x=\dfrac53$ 或 $x=\dfrac73$,
此时 $N$ 点坐标为 $\left(\dfrac53,0\right)$ 或 $\left(\dfrac73,0\right)$;
② 当 $\dfrac{MN}{BC }=\dfrac{ON}{ AB}$ 时,则有 $\dfrac{\left|-x^2+2x\right|}{3\sqrt{2} }=\dfrac{\left|x\right|}{\sqrt{2} }$,即 $\left|x\right|\left|-x+2\right|=3\left|x\right|$,
所以 $\left|-x+2\right|=3$,即 $-x+2=\pm 3$,解得 $x=5$ 或 $x=-1$,
此时 $N$ 点坐标为 $\left(-1,0\right)$ 或 $\left(5,0\right)$,
综上可知存在满足条件的 $N$ 点,其坐标为 $\left(\dfrac53,0\right)$ 或 $\left(\dfrac73,0\right)$ 或 $\left(-1,0\right)$ 或 $\left(5,0\right)$.
答案
解析
备注