如图，在平面直角坐标系 $xOy$ 中，点 $A,B,C$ 分别为坐标轴上的三个点，且 $OA=1$，$OB=3$，$OC=4$．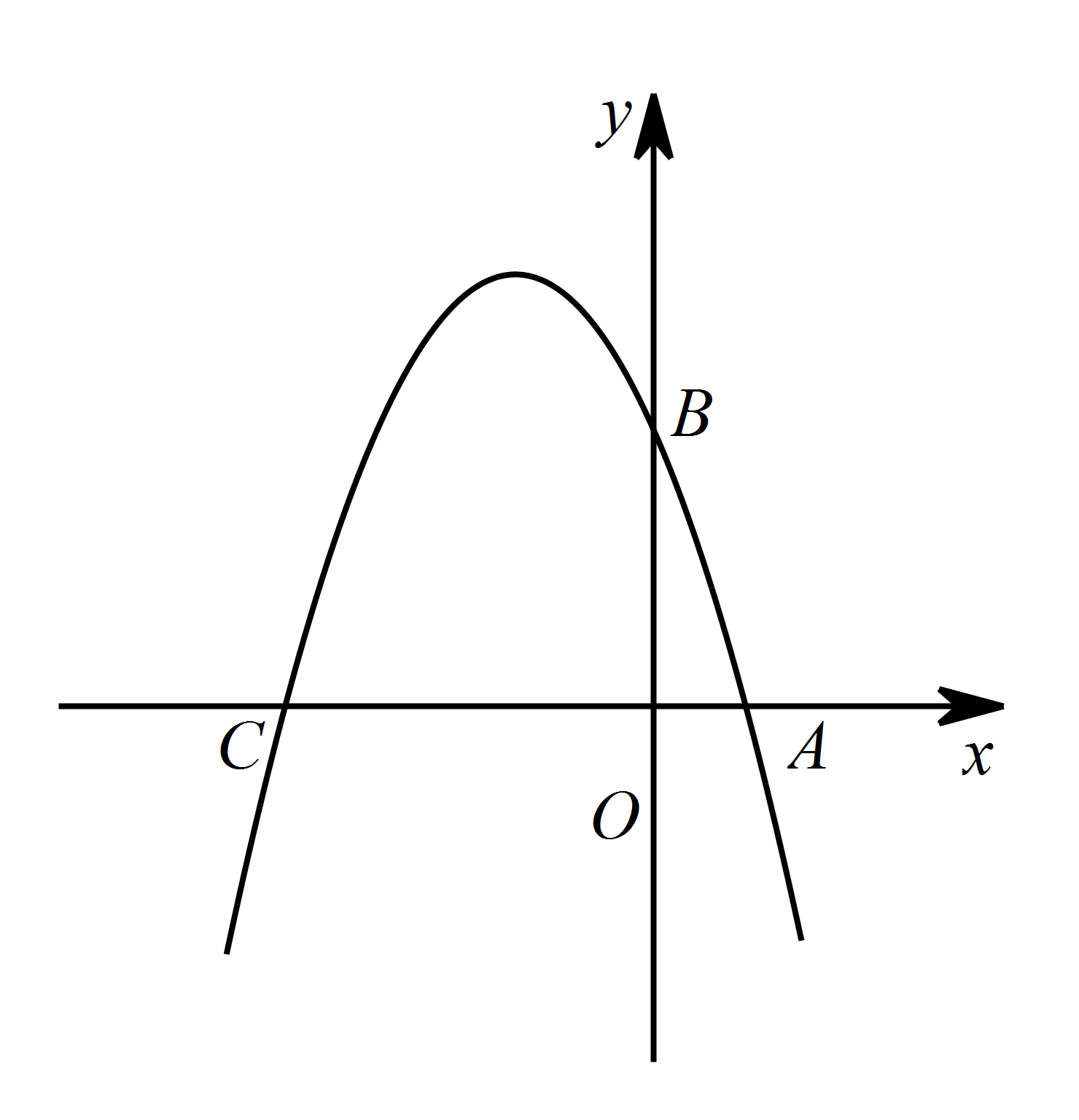
【难度】
【出处】
无
【标注】
-
在平面直角坐标系 $xOy$ 中是否存在一点 $P$，使得以点 $A,B,C,P$ 为顶点的四边形为菱形？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由；标注答案当点 $P$ 的坐标为 $\left(5,3\right)$ 时，以点 $A,B,C,P$ 为顶点的四边形为菱形解析因为 $OB=3$，$OC=4$，
所以 $BC=AC=5$．
① 当 $BP$ 平行且等于 $AC$ 时，四边形 $ACBP$ 为菱形．
所以 $BP=AC=5$，且点 $P$ 到 $x$ 轴的距离等于 $OB $．
所以点 $P$ 的坐标为 $\left(5,3\right) $．
② 当点 $P$ 在第二、三象限时，以点 $A,B,C,P$ 为顶点的四边形只能是平行四边形，不是菱形，
综上可得，当点 $P$ 的坐标为 $\left(5,3\right)$ 时，以点 $A,B,C,P$ 为顶点的四边形为菱形． -
若点 $M$ 为该抛物线上一动点，在 $(2)$ 的条件下，请求出当 $\left|PM-AM\right|$ 的最大值时点 $M$ 的坐标，并直接写出 $\left|PM-AM\right|$ 的最大值．标注答案$\left|PM-AM\right|$ 的最大值为 $5$解析设抛物线的解析式为 $y=ax^2+bx+c$，
将 $A,B,C$ 坐标代入解析式，得
$\begin{cases}a+b+c=0,\\c=3,\\16a-4b+c=0.\end{cases}$ 解得 $\begin{cases}a=-\dfrac34,\\b=-\dfrac94,\\c=3.\end{cases}$
所以经过 $A,B,C$ 三点的抛物线的解析式为 $y=-\dfrac34x^2-\dfrac94x+3$．
设直线 $PA$ 的解析式为 $y=kx+b\left(k\ne 0\right) $，
将 $ A,P$ 坐标代入解析式，得
$\begin{cases}5k+b=3,\\k+b=0.\end{cases}$
解得 $\begin{cases}k=\dfrac34,\\b=-\dfrac34.\end{cases}$
所以直线 $PA$ 的解析式为 $y=\dfrac34x-\dfrac34$．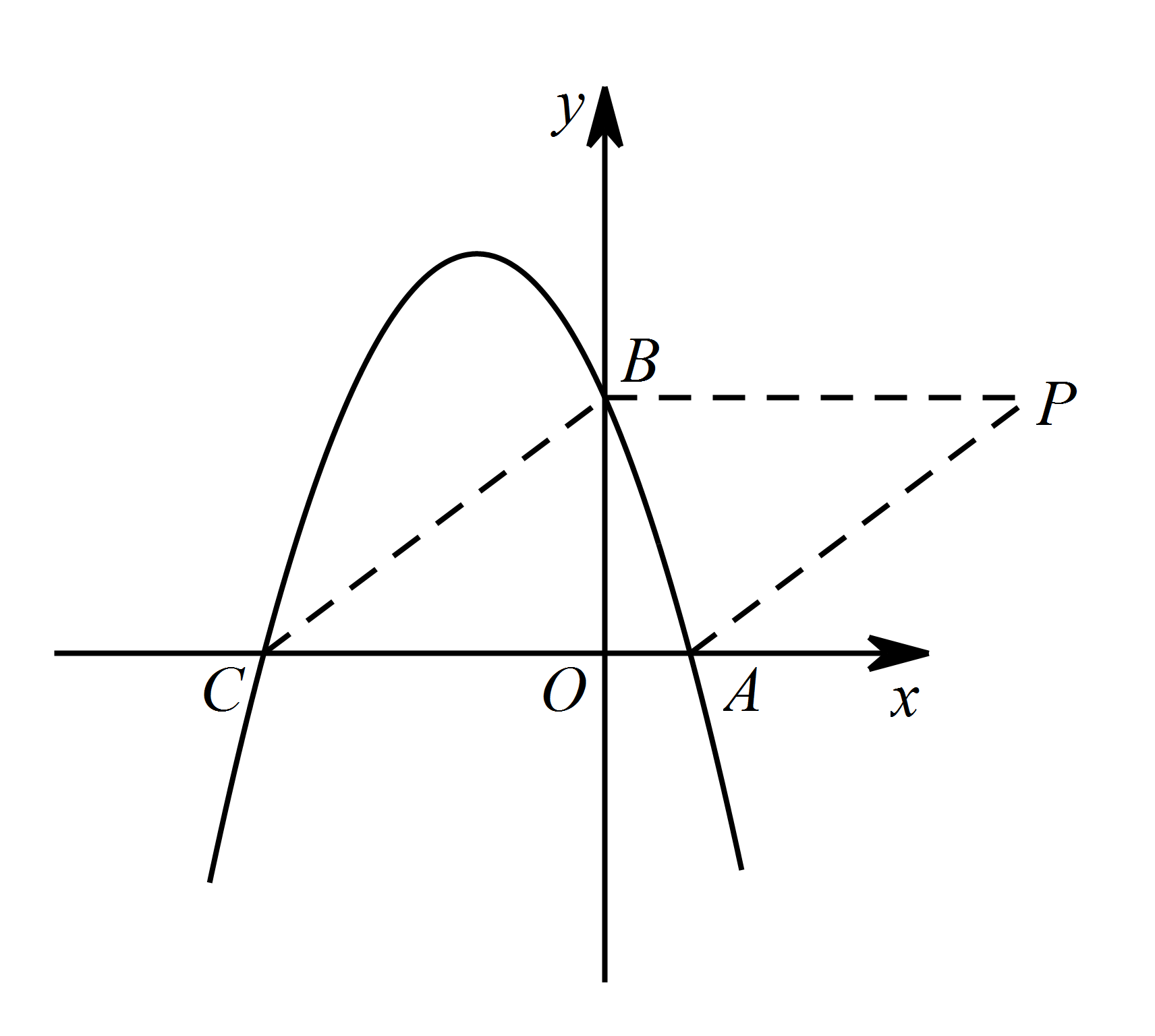
当点 $M$ 与点 $P,A$ 不在同一直线上时，根据三角形的三边关系 $\left|PM-AM\right|<PA$；
当点 $M$ 与点 $P,A$ 在同一直线上时，$\left|PM-AM\right|=PA$．
所以当点 $M$ 与点 $P,A$ 在同一直线上时，$\left|PM-AM\right|$ 的值最大，即点 $M$ 为直线 $PA$ 与抛物线的交点．
解方程组 $\begin{cases}y=\dfrac34x-\dfrac34,\\y=-\dfrac34x^2-\dfrac94x+3.\end{cases}$ 得 $\begin{cases}x_1=1,\\ y_1=0.\end{cases}\begin{cases}x_2=-5,\\y_2=-\dfrac92.\end{cases}$
所以点 $M$ 的坐标为 $\left(1,0\right)$ 或 $\left(-5,-\dfrac92\right)$ 时，$\left|PM-AM\right|$ 的值最大，此时 $\left|PM-AM\right|$ 的最大值为 $5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
