在平面直角坐标系 $xOy$ 中,$\odot C$ 的半径为 $r$,$P$ 是与圆心 $C$ 不重合的点,点 $P$ 关于 $\odot O$ 的反称点的定义如下:若在射线 $CP$ 上存在一点 $P'$,满足 $CP+CP'=2r$,则称 $P'$ 为点 $P$ 关于 $\odot C$ 的反称点,下图为点 $P$ 及其关于 $\odot C$ 的反称点 $P'$ 的示意图.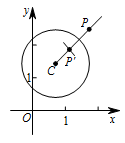
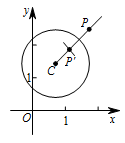
【难度】
【出处】
无
【标注】
-
当 $ \odot O$ 的半径为 $1$ 时.
$(1)$ 分别判断点 $M\left(2,1\right)$,$N\left(\dfrac{3}{2},0\right)$,$T\left(1,\sqrt 3 \right)$ 关于 $\odot O$ 的反称点是否存在,若存在?求其坐标;
$(2)$ 点 $P$ 在直线 $y=-x+2$ 上,若点 $P$ 关于 $\odot O$ 的反称点 $P'$ 存在,且点 $P'$ 不在 $x$ 轴上,求点 $P$ 的横坐标的取值范围;标注答案$(1)$ $M\left(2,1\right)$ 关于 $\odot O$ 的反称点不存在,
$N\left(\dfrac32,0\right)$ 关于 $\odot O$ 的反称点存在,反称点 $N'\left(\dfrac12,0\right)$,
$T\left(1,\sqrt3\right)$ 关于 $\odot O$ 的反称点存在,反称点 $T'\left(0,0\right)$.
$(2)$ 点 $P$ 的横坐标满足 $0<x<2$解析$(2)$ 设点 $P$ 的坐标为 $\left(x,-x+2\right)$,由题意知 $OP\leqslant 2$,
所以 $OP^2=x^2+\left(-x+2\right)^2=2x^2-4x+4\leqslant4$.
整理得 $x\left(x-2\right)\leqslant0$,所以 $0\leqslant x\leqslant2$.
当 $x=2$ 时,$P\left(2,0\right)$,$P'\left(0,0\right)$ 不符合题意;
当 $x=0$ 时,$P\left(0,2\right)$,$P'\left(0,0\right)$ 不符合题意.
所以点 $P$ 的横坐标满足 $0<x<2$. -
当 $\odot C$ 的圆心在 $x$ 轴上,半径为 $1$,直线 $y=-\dfrac{\sqrt 3}{3}x+2\sqrt 3$ 与 $x$ 轴,$y$ 轴分别交于点 $A,B$,若线段 $AB$ 上存在点 $P$,使得点 $P$ 关于 $\odot C$ 的反称点 $P'$ 在 $\odot C$ 的内部,求圆心 $C$ 的横坐标的取值范围.标注答案圆心 $C$ 的横坐标的取值范围 $2\leqslant x\leqslant 8$解析由题意得 $A\left(6,0\right)$,$B\left(0,2\sqrt3\right)$,
所以 $\dfrac{OA}{OB}=\sqrt3$,$\angle OAB=30^\circ$.
设 $C\left(x,0\right)$.
① 当 $C$ 在 $OA$ 上时,作 $CH\perp AB$ 于 $H$,则 $CH\leqslant CP\leqslant 2r=2$. 所以 $AC\leqslant4$,
所以 $AC\leqslant4$,
所以点 $C$ 的横坐标 $x\geqslant2$,当 $x=2$ 时,$C$ 点坐标 $\left(2,0\right)$,$H$ 点的反称点 $H'\left(2,0\right)$ 在圆的内部;
② 当 $C$ 在 $A$ 点右侧时,$C$ 到线段 $AB$ 的距离为 $AC$ 长,$AC$ 最大值为 $2$. 所以点 $C$ 的横坐标 $x\leqslant8$.
所以点 $C$ 的横坐标 $x\leqslant8$.
综上所述,圆心 $C$ 的横坐标的取值范围 $2\leqslant x\leqslant 8$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2