如图，抛物线 $y=x^2-4x$ 与 $x$ 轴交于 $O,A$ 两点，$P$ 为抛物线上一点，过点 $P$ 的直线 $y=x+m$ 与对称轴交于点 $Q$．
【难度】
【出处】
无
【标注】
-
若两个三角形面积满足 $S_{\triangle POQ}=\dfrac 13S_{\triangle PAQ}$，求 $m$ 的值；标注答案当 $m=-1$ 或 $2$ 时，$S_{\triangle POQ}=\dfrac 13S_{\triangle PAQ}$解析由抛物线的解析式可得点 $A$ 的坐标为 $(4,0)$．
过点 $O,A$ 作 $PQ$ 的垂线，垂足分别是 $E,F$，令直线 $PQ$ 交 $x$ 轴于点 $B$．
若 $S_{\triangle POQ}=\dfrac 13S_{\triangle PAQ}$，
所以 $\dfrac 12 OE\cdot PQ=\dfrac 13\times \dfrac 12 AF\cdot PQ$，
即 $OE=\dfrac 13 AF$．
显然当点 $B$ 在 $OA$ 延长线上时，$OE=\dfrac 13 AF$ 不成立．
① 当点 $B$ 落在线段 $OA$ 上时，如图．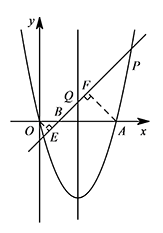
由 $\triangle OBE\backsim \triangle ABF$，得 $\dfrac{OB}{AB}=\dfrac{OE}{AF}=\dfrac 13$．
所以 $AB=3OB$，即 $OB=\dfrac 14OA=1$．
所以点 $B$ 的坐标为 $\left(1,0\right)$．
将其代入直线解析式可得 $ m=-1$．
② 当点 $B$ 落在 $AO$ 的延长线上时，如图．
同理可得 $OB=\dfrac{1}{2}OA=2$．
所以点 $B$ 的坐标为 $\left(-2,0\right)$．
将其代入直线解析式可得 $ m=2$．
综上可得，当 $m=-1$ 或 $2$ 时，$S_{\triangle POQ}=\dfrac 13S_{\triangle PAQ}$ -
当点 $P$ 在 $x$ 轴下方的抛物线上时，过点 $C\left(2,2\right)$ 的直线 $AC$ 与直线 $PQ$ 交于点 $D$，求：
$(1)$ $PD+DQ$ 的最大值；
$(2)$ $PD\cdot DQ$ 的最大值．标注答案$(1)$ $PD+DQ$ 的最大值为 $6\sqrt 2$；
$(2)$ $PD\cdot DQ$ 的最大值为 $18$解析$(1)$ 如图，过点 $C$ 作 $CH\parallel x$ 轴交直线 $PQ$ 于点 $H$，过点 $P$ 作 $PM\perp CH$ 于点 $M$．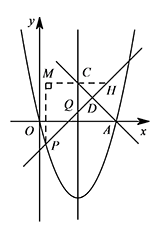
易证 $AC\perp PQ$，所以 $DQ=DC=DH$，
从而 $PD+DQ=PH$．
由辅助线的作法可得 $PH=\sqrt 2PM$，
所以当 $PM$ 最大时，$PH$ 最大．
故当点 $P$ 在抛物线顶点处时 $PM$ 取最大值，此时 $PM=6$．
所以 $PD+DQ$ 的最大值为 $6\sqrt 2$．
$(2)$ 由 $(1)$ 可知 $PD+DQ\leqslant 6\sqrt 2$．
设 $PD=a$，则 $DQ\leqslant 6\sqrt 2-a$．
所以 $PD\cdot DQ\leqslant a\left(6\sqrt 2-a\right)=-a^2+6\sqrt 2a=-\left(a-3\sqrt 2\right)^2+18$．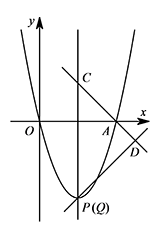
当点 $P$ 在抛物线的顶点时，$a=PD=\dfrac{PC}{\sqrt 2}=3\sqrt 2$，
所以当点 $P$ 在抛物线的顶点时，$PD\cdot DQ$ 的最大值为 $18$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
