在平面直角坐标中，$\triangle ABC$ 三个顶点坐标为 $A\left(-\sqrt{3},0\right)$，$B\left(\sqrt{3},0\right)$，$C\left(0,3\right)$．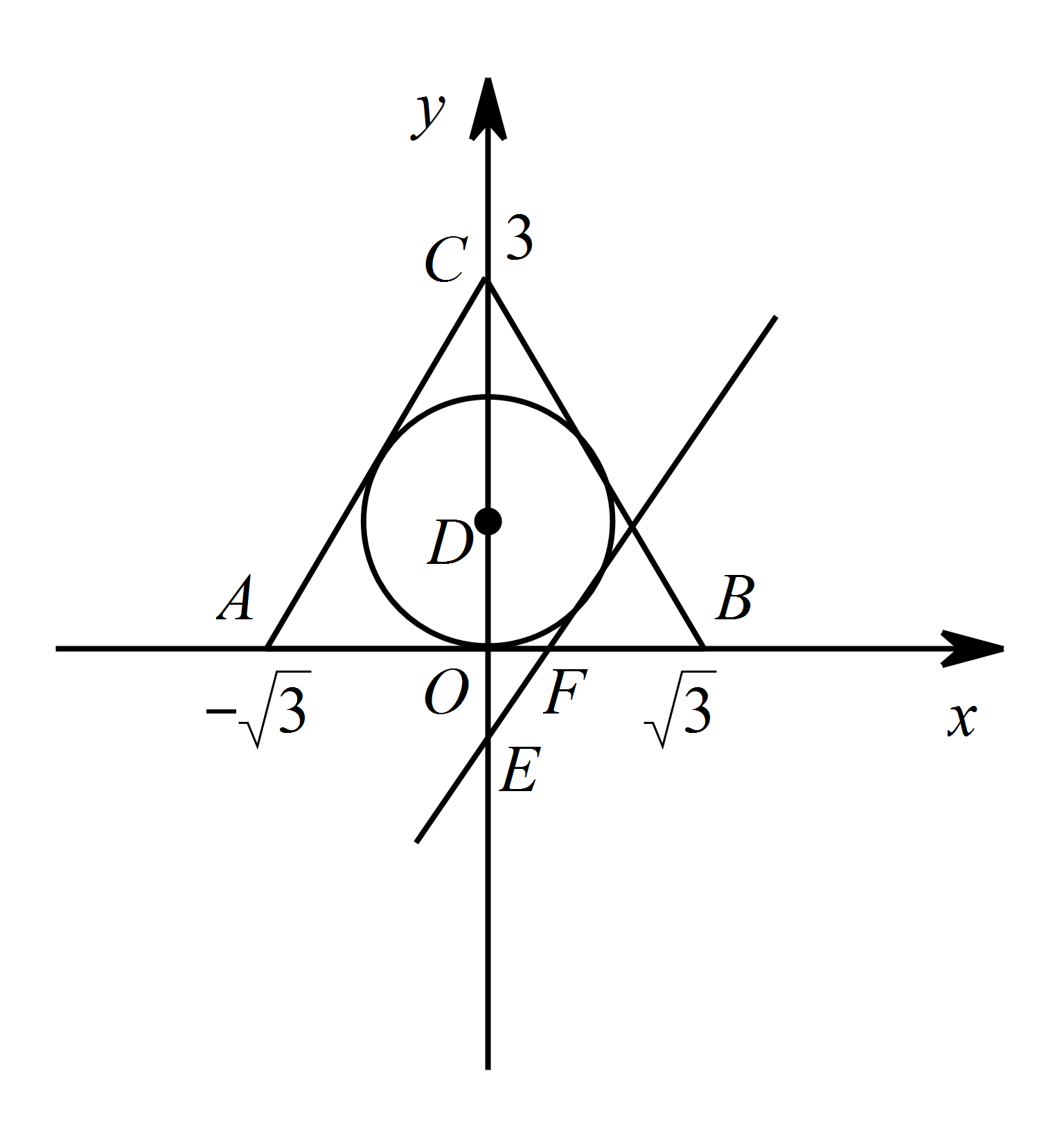
【难度】
【出处】
无
【标注】
-
求 $\triangle ABC$ 内切圆 $\odot D$ 的半径．标注答案$\triangle ABC$ 内切圆 $\odot D$ 的半径为 $1$解析连接 $BD$，
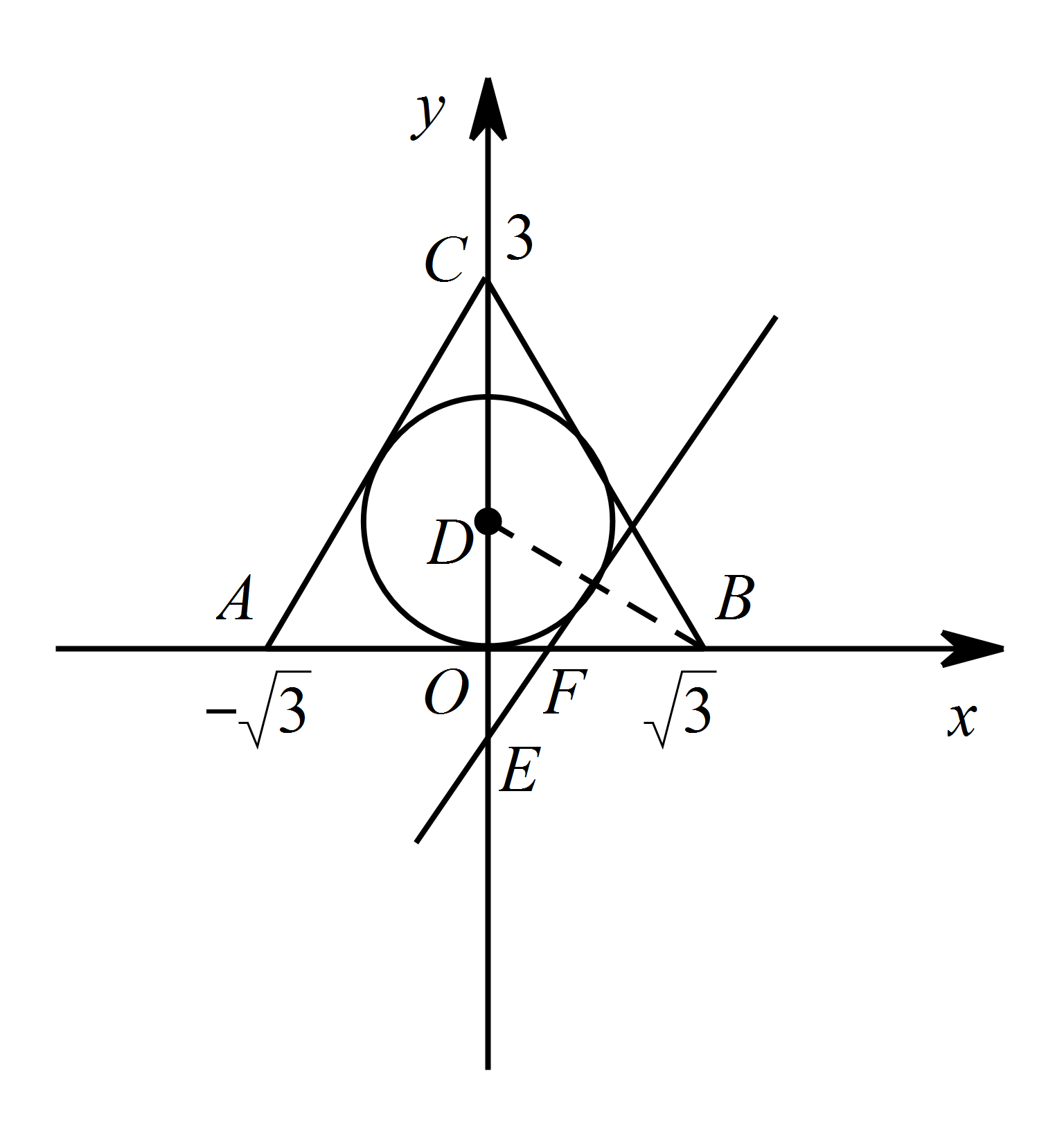因为 $ B\left(\sqrt{3},0\right)$，$C\left(0,3\right)$，
所以 $ OB=\sqrt{3}$，$OC=3$，
所以 $ \tan \angle CBO=\dfrac{OC}{ OB}=\sqrt{3}$，
所以 $ \angle CBO=60^\circ $．
因为点 $D$ 是 $\triangle ABC$ 的内心，
所以 $ BD$ 平分 $\angle CBO$，
所以 $\angle DBO=30^\circ $，
所以 $ \tan \angle DBO=\dfrac{OD}{ OB}$，
所以 $OD=1$，
所以 $\triangle ABC$ 内切圆 $\odot D$ 的半径为 $1$． -
过点 $E\left(0,-1\right)$ 的直线与 $\odot D$ 相切于点 $F$（点 $F$ 在第一象限），求直线 $EF$ 的解析式．标注答案直线 $EF$ 的解析式为 $y=\sqrt{3}x-1$解析连接 $DF$，
过点 $F$ 作 $FG\perp y$ 轴于点 $G$，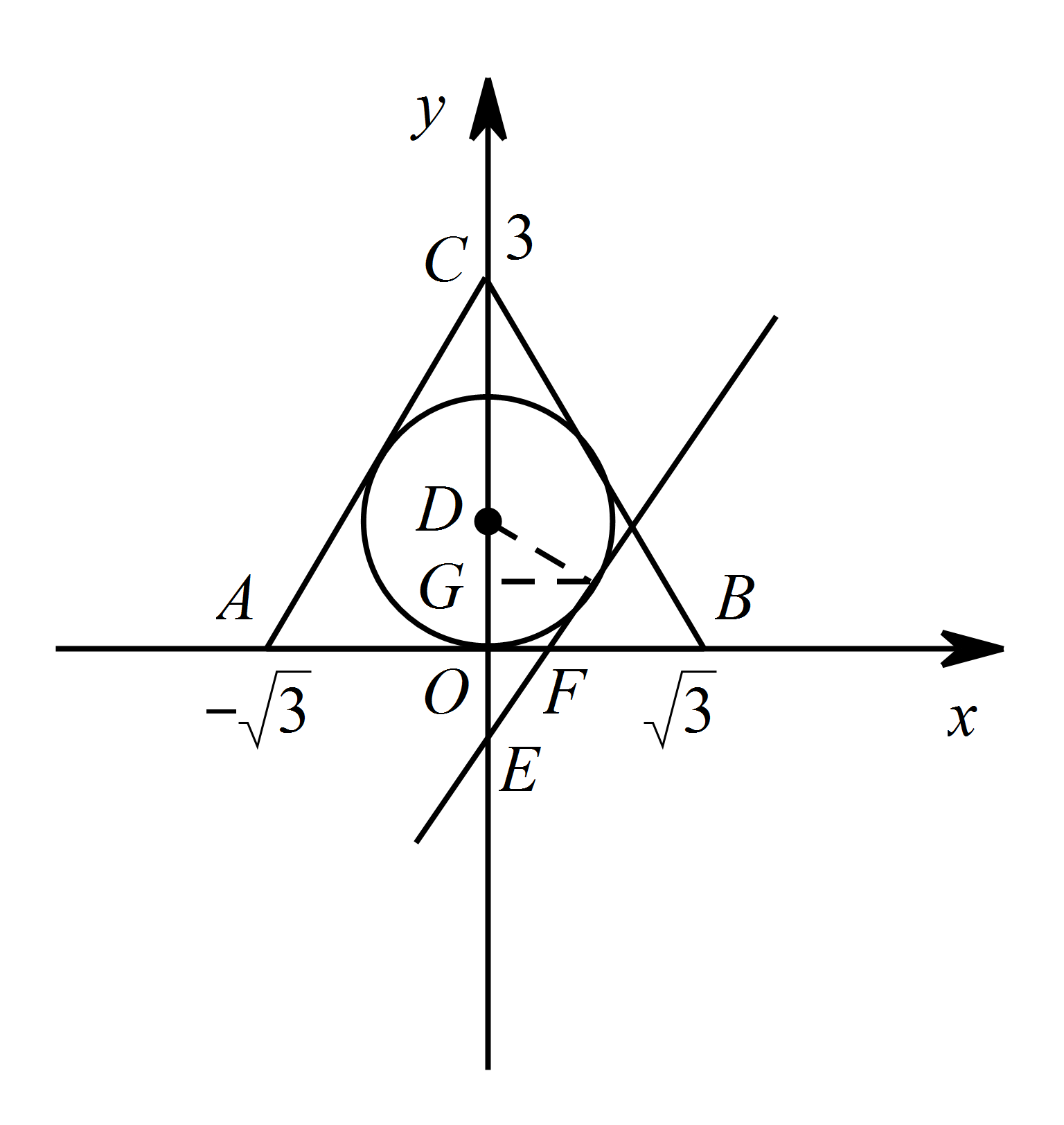
因为 $E\left(0,-1\right)$
所以 $ OE=1$，$DE=2$，
因为直线 $EF$ 与 $\odot D$ 相切，
所以 $ \angle DFE=90^\circ $，$DF=1$，
所以 $ \sin \angle DEF=\dfrac{DF}{ DE}$，
所以 $\angle DEF=30^\circ $，
所以 $\angle GDF=60^\circ $．
在 $\mathrm {Rt}\triangle DGF$ 中，$\angle DFG=30^\circ $，
所以 $ DG=\dfrac{1}{2 }$．
由勾股定理可求得：$GF=\dfrac{\sqrt{3}}{ 2}$，
所以 $ F\left(\dfrac{\sqrt{3}}{ 2},\dfrac{1}{ 2}\right)$．
设直线 $EF$ 的解析式为：$y=kx+b$，
所以 $\begin{cases}b=-1,\\\dfrac{1}{ 2}=\dfrac{\sqrt{3}}{2 }k+b,\end{cases}$
所以直线 $EF$ 的解析式为 $y=\sqrt{3}x-1$． -
以 $(2)$ 为条件，$P$ 为直线 $EF$ 上一点，以 $P$ 为圆心，以 $2\sqrt{7}$ 为半径作 $\odot P$．若 $\odot P$ 上存在一点到 $\triangle ABC$ 三个顶点的距离相等，求此时圆心 $P$ 的坐标．标注答案圆心 $P$ 的坐标为 $\left(2\sqrt{3},5\right)$ 或 $\left(-\sqrt{3},-4\right)$解析因为 $ \odot P$ 上存在一点到 $\triangle ABC$ 三个顶点的距离相等，
所以该点必为 $\triangle ABC$ 外接圆的圆心，
由 $(1)$ 可知：$\triangle ABC$ 是等边三角形，
所以 $\triangle ABC$ 外接圆的圆心为点 $D$，
所以 $DP=2\sqrt{7}$．
设直线 $EF$ 与 $x$ 轴交于点 $H$，
所以令 $y=0$ 代入 $y=\sqrt{3}x-1$，
所以 $ x=\dfrac{\sqrt{3}}{ 3}$，
所以 $H\left(\dfrac{\sqrt{3}}{ 3},0\right)$，
所以 $ FH=\dfrac{\sqrt{3}}{ 3}$．
当 $P$ 在 $x$ 轴上方时，
过点 $P_{1}$ 作 $P_{1}M\perp x$ 轴于 $M$．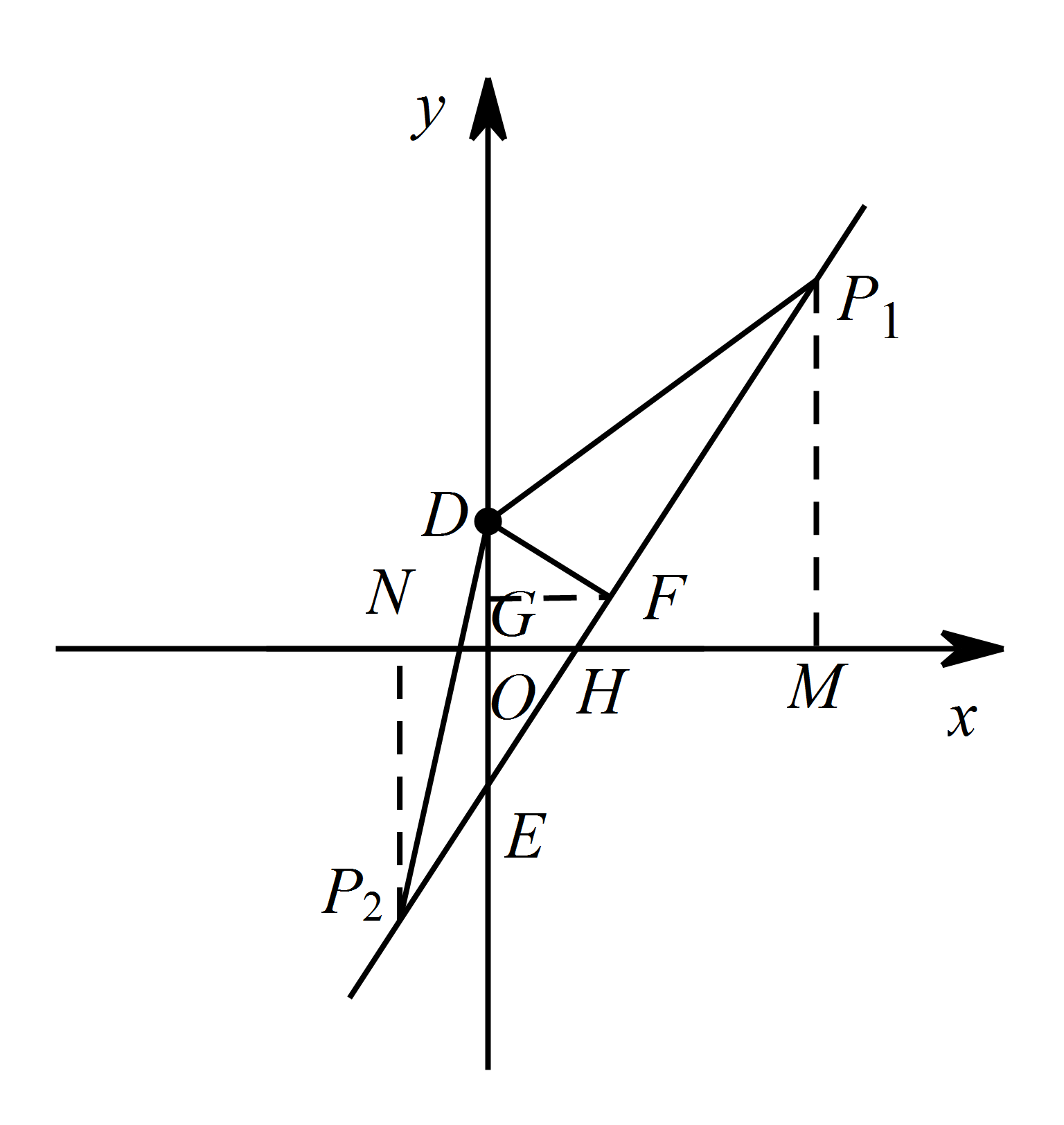
由勾股定理可求得：$P_{1}F=3\sqrt{3}$，
所以 $P_{1}H=P_{1}F+FH=\dfrac{10\sqrt{3}}{ 3}$．
因为 $ \angle DEF=\angle HP_{1}M=30^\circ $，
所以 $HM=\dfrac{1}{ 2}P_{1}H=\dfrac{5\sqrt{3}}{ 3}$，$P_{1}M=5$，
所以 $ OM=2\sqrt{3}$，
所以 $ P_{1}\left(2\sqrt{3},5\right)$．
当 $P$ 在 $x$ 轴下方时，
过点 $P_{2}$ 作 $P_{2}N\perp x$ 轴于点 $N$．
由勾股定理可求得：$P_{2}F=3\sqrt{3}$，
所以 $ P_{2}H=P_{2}F-FH=\dfrac{8\sqrt{3}}{ 3}$，
所以 $ \angle DEF=30^\circ $，
所以 $ \angle OHE=60^\circ $，
所以 $ \sin \angle OHE=\dfrac{P_{2}N}{ P_{2}H}$，
所以 $P_{2}N=4$．
令 $y=-4$ 代入 $y=\sqrt{3}x-1$，
所以 $x=-\sqrt{3}$，
所以 $ P_{2}\left(-\sqrt{3},-4\right)$，
综上所述，若 $\odot P$ 上存在一点到 $\triangle ABC$ 三个顶点的距离相等，此时圆心 $P$ 的坐标为 $\left(2\sqrt{3},5\right)$ 或 $\left(-\sqrt{3},-4\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
