如图 ①，直线 $y=\dfrac {4}{3}x+4$ 交于 $x$ 轴于点 $A$，交 $y$ 轴于点 $C$，过 $A$，$C$ 两点的抛物线 $F_{1}$ 交 $x$ 轴于另一点 $B\left(1,0\right)$．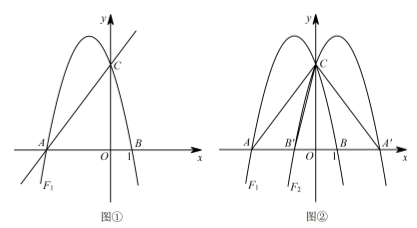
【难度】
【出处】
无
【标注】
-
若点 $M$ 是抛物线 $F_{1}$ 位于第二象限图象上的一点，设四边形 $MAOC$ 和 $\triangle BOC$ 的面积分别为 $S_{四边形MAOC}$ 和 $S_{\triangle BOC}$，记 $S=S_{四边形MAOC}-S_{\triangle BOC}$，求 $S$ 最大时点 $M$ 的坐标及 $S$ 的最大值；标注答案$M\left(-\dfrac {3}{2},5\right)$解析令 $y=0$ 代入 $y=\dfrac {4}{3}x+4$，
所以 $ x=-3$，$A\left(-3,0\right)$，
令 $x=0$，代入 $y=\dfrac {4}{3}x+4$，
所以 $y=4$，
所以 $ C\left(0,4\right)$，
设抛物线 $F_{1}$ 的解析式为：$y=a\left(x+3\right)\left(x-1\right)$，
把 $C\left( 0,4\right)$ 代入上式得，$a=-\dfrac {4}{3}$，
所以 $ y=-\dfrac {4}{3}x^{2}-\dfrac {8}{3}x+4$．
如图 ①，设点 $M\left(a,-\dfrac {4}{3}a^{2}-\dfrac {8}{3}a+4\right)$，其中 $-3<a<0$．
因为 $B\left(1,0\right)$，$C\left(0,4\right)$，
所以 $ OB=1$，$OC=4$，
所以 $S_{\triangle BOC}=\dfrac {1}{2}OB\cdot OC=2$，
过点 $M$ 作 $MD\perp x$ 轴于点 $D$，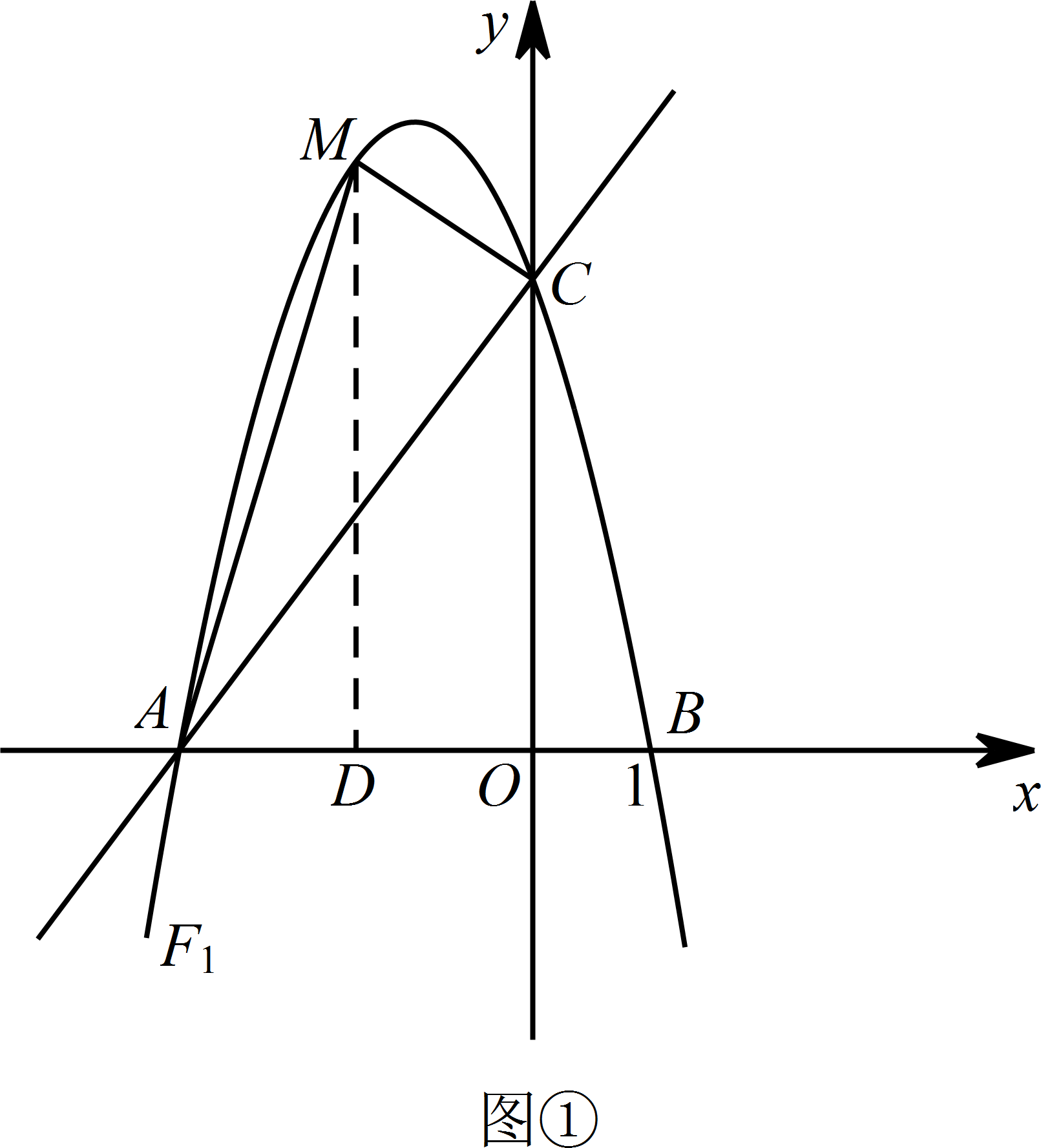
所以 $ MD=-\dfrac {4}{3}a^{2}-\dfrac {8}{3}a+4$，$AD=a+3$，$OD=-a$，
所以
$\begin{split}
S_{四边形MAOC}&=\dfrac {1}{2}AD\cdot MD+\dfrac {1}{2}\left(MD+OC\right)\cdot OD\\
&=\dfrac {1}{2}AD\cdot MD+\dfrac {1}{2}OD\cdot MD+\dfrac {1}{2}OD\cdot OC\\
&=\dfrac {1}{2}MD\left( {AD + OD} \right) + \dfrac {1}{2}OD \cdot OC\\
&=\dfrac {1}{2}MD \cdot OA + \dfrac {1}{2}OD \cdot OC\\
&=\dfrac {1}{2}\times 3\left(-\dfrac {4}{3}a^{2}-\dfrac {8}{3}a+4\right)+\dfrac {1}{2}\times 4\times \left(-a\right)\\
&=-2a^{2}-6a+6.\end{split}$
所以
$\begin{split}
S&=S_{四边形MAOC}-S_{\triangle BOC}\\
&=\left(-2a^{2}-6a+6\right)-2\\
&=-2a^{2}-6a+4\\
&=-2\left(a+\dfrac {3}{2}\right)^{2}+\dfrac {17}{2}.\end{split}$
所以 当 $a=-\dfrac {3}{2}$ 时，
$S$ 有最大值，最大值为 $\dfrac {17}{2}$，
此时，$M\left(-\dfrac {3}{2},5\right)$． -
如图 ②，将抛物线 $F_{1}$ 沿 $y$ 轴翻折并“复制”得到抛物线 $F_{2}$，点 $A$，$B$ 与 $(2)$ 中所求的点 $M$ 的对应点分别为 $A'$，$B'$，$M'$，过点 $M'$ 作 $M'E\perp x$ 轴于点 $E$，交直线 $A'C$ 于点 $D$，在 $x$ 轴上是否存在点 $P$，使得以 $A'$，$D$，$P$ 为顶点的三角形与 $\triangle AB'C$ 相似？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由．标注答案当以 $A'$，$D$，$P$ 为顶点的三角形与 $\triangle AB'C$ 相似时，点 $P$ 的坐标为 $\left(2,0\right)$ 或 $\left(-\dfrac {13}{4},0\right)$解析如图 ②，
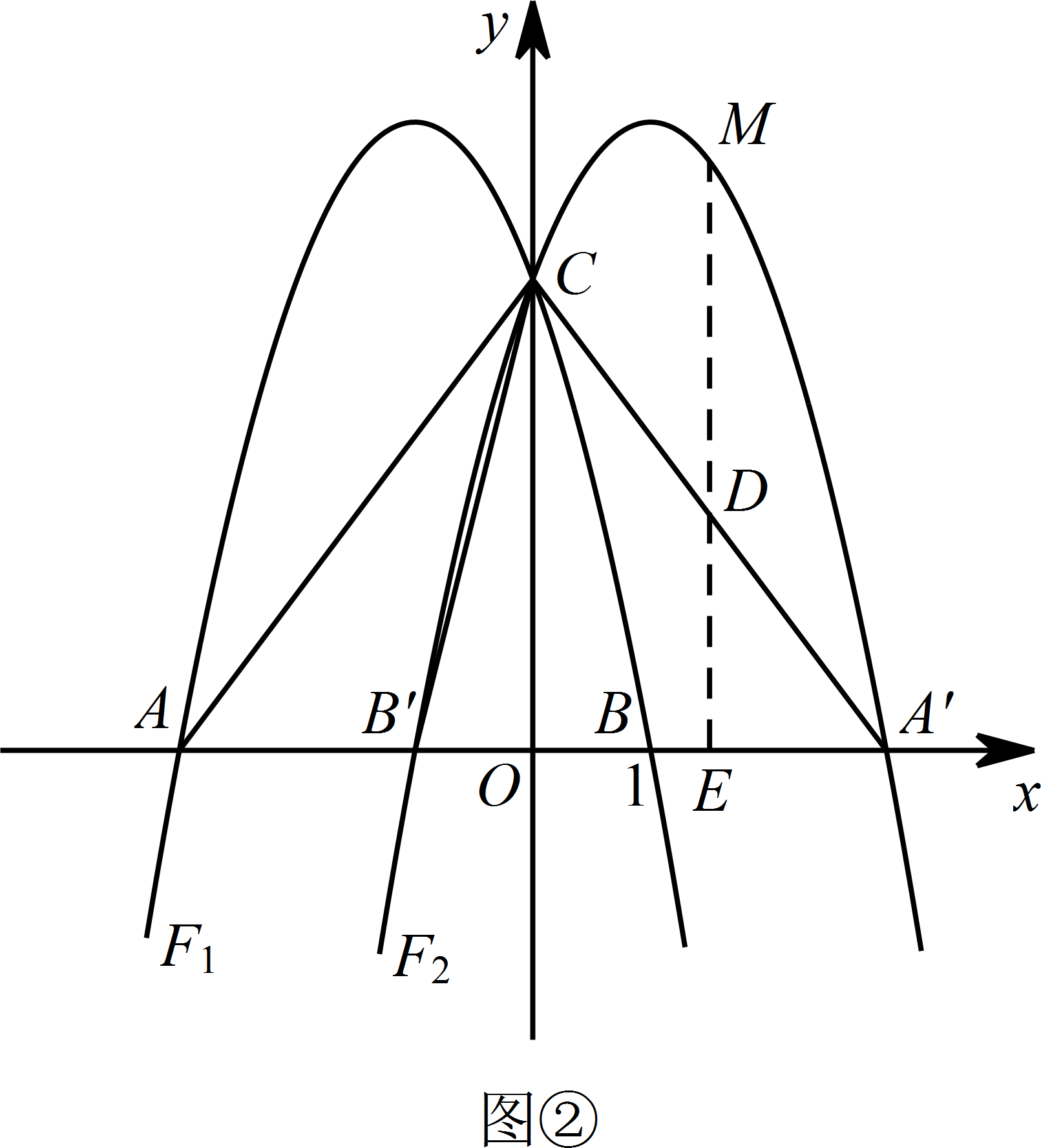由题意知 $M'\left(\dfrac {3}{2},5\right)$，$B'\left(-1,0\right)$，$A'\left(3,0\right)$
所以 $AB'=2$．
设直线 $A'C$ 的解析式为 $y=kx+b$，
把 $A'\left(3,0\right)$ 和 $C\left(0,4\right)$ 代入 $y=kx+b$，
得 $\begin{cases}
b = 4,\\
0 = 3k + b,\end{cases}$ 解得 $\begin{cases}k= - \dfrac {4}{3} \\
b=4, \\
\end{cases}$
所以 $ y=-\dfrac {4}{3}x+4$．
令 $x=\dfrac {3}{2}$ 代入 $y=-\dfrac {4}{3}x+4$，
所以 $y=2$，
所以 $D\left( {\dfrac {3}{2},2} \right)$．
由勾股定理分别可求得 $AC=5$，$DA'=\dfrac {5}{2}$．
设 $P\left(m,0\right)$，
当 $m<3$ 时，
此时点 $P$ 在 $A'$ 的左边，
所以 $ \angle DA'P=\angle CAB'$．
当 $\dfrac {DA'}{PA'} = \dfrac {AC}{AB'}$ 时，$\triangle DA'P\backsim \triangle CAB'$，
此时，$\dfrac {5}{2}=\dfrac {5}{2}\left(3-m\right)$，
解得 $m=2$，
所以 $ P\left(2,0\right)$．
当 $\dfrac {DA'}{PA'} = \dfrac {AB'}{AC}$ 时，$\triangle DA'P\backsim \triangle B'AC$，
此时，$\dfrac {5}{2}=\dfrac {2}{5} \left(3-m\right)$，
$m=-\dfrac {13}{4}$，
所以 $ P\left(-\dfrac {13}{4},0\right)$．
当 $m>3$ 时，
此时，点 $P$ 在 $A'$ 右边，
由于 $\angle CB'O\neq \angle DA'E$，
所以 $ \angle AB'C\neq \angle DA'P$．
所以此情况，$\triangle DA'P与\triangle B'AC$ 不能相似，
综上所述，当以 $A'$，$D$，$P$ 为顶点的三角形与 $\triangle AB'C$ 相似时，点 $P$ 的坐标为 $\left(2,0\right)$ 或 $\left(-\dfrac {13}{4},0\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
