如图，抛物线 $y=\dfrac 13 x^2+\dfrac 23 x-5$ 与 $x$ 轴交于点 $A(-5,0)$ 和点 $B(3,0)$，与 $y$ 轴交于点 $C$．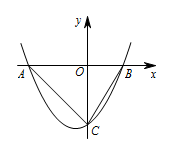
【难度】
【出处】
无
【标注】
-
若点 $E$ 为 $x$ 轴下方抛物线上的一动点，当 $S_{\triangle ABE}=S_{\triangle ABC}$ 时，求点 $E$ 的坐标；标注答案在 $y=\dfrac 13 x^2+\dfrac 23 x-5$ 中，令 $x=0$ 可得 $y=-5$，
所以 $C(0,-5)$，
因为 $S_{\triangle ABE}=S_{\triangle ABC}$，且 $E$ 点在 $x$ 轴下方，
所以 $E$ 点纵坐标和 $C$ 点纵坐标相同，
当 $y=-5$ 时，代入可得 $\dfrac 13 x^2+\dfrac 23 x=-5$，解得 $x=-2$ 或 $x=0$（舍去），
所以 $E$ 点坐标为 $(-2,-5)$解析略 -
在 $(1)$ 的条件下，抛物线上是否存在点 $P$，使 $\angle BAP=\angle CAE$？若存在，求出点 $P$ 的横坐标；若不存在，请说明理由．标注答案假设存在满足条件的 $P$ 点，其坐标为 $(m, \dfrac 13 m^2+\dfrac 23 m-5)$，
如图，连接 $AP$、$CE$、$AE$，过 $E$ 作 $ED\perp AC$ 于点 $D$，过 $P$ 作 $PQ\perp x$ 轴于点 $Q$，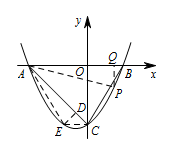
则 $AQ=AO+OQ=5+m$，$PQ=\left| \dfrac 13m^2+\dfrac 23 m-5\right|$，
在 $\mathrm {Rt}\triangle AOC$ 中，$OA=OC=5$，则 $AC=5$，$\angle ACO=\angle DCE=45^\circ$，
由 $(2)$ 可得 $EC=2$，在 $\mathrm {Rt}\triangle EDC$ 中，可得 $DE=DC=\sqrt 2$，
所以 $AD=AC-DC=5\sqrt 2 -\sqrt 2 =4$，
当 $\angle BAP=\angle CAE$ 时，则 $\triangle EDA\backsim \triangle PQA$，
所以 $\dfrac{ED}{AD}=\dfrac{PQ}{AQ}$，即 $\dfrac{\sqrt 2}{4\sqrt 2} =\dfrac{\left|\dfrac 13m^2+\dfrac 23m-5\right|}{5+m}$，
所以 $\dfrac 13 m^2+\dfrac 23 m-5= (5+m)$ 或 $\dfrac 13 m^2+\dfrac 23 m-5=-\dfrac 14 (5+m)$，
当 $\dfrac 13 m^2+\dfrac 23 m-5= (5+m)$ 时，整理可得 $4m^2-5m-75=0$，解得 $m=\dfrac{15}{4}$ 或 $m=-5$（与 $A$ 点重合，舍去），
当 $\dfrac 13 m^2+\dfrac 23 m-5=-\dfrac 14 (5+m)$ 时，整理可得 $4m^2+11m-45=0$，解得 $m=\dfrac 94$ 或 $m=-5$（与 $A$ 点重合，舍去），
所以存在满足条件的点P，其横坐标为 $\dfrac 94$ 或 $\dfrac{15}{4}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
