如图，在平面直角坐标系中，抛物线经过点 $A\left(0,4\right),B\left(1,0\right),C\left(5,0\right)$，其对称轴与 $x$ 轴相交于点 $M$．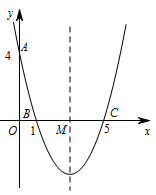
【难度】
【出处】
无
【标注】
-
在此抛物线的对称轴上是否存在一点 $P$，使 $\triangle PAB$ 的周长最小？若存在，请求出点 $P$ 的坐标；若不存在，请说明理由；标注答案存在，当点 $P$ 的坐标为 $\left(3, \dfrac{8}{5} \right)$ 时，$\triangle PAB$ 的周长最小解析如图，连接 $AC$ 交对称轴于点 $P$，连接 $BP,AB$．
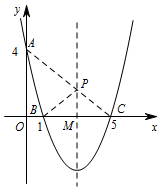因为点 $B$ 与点 $C$ 关于对称轴对称，
所以 $ PB=PC$，且对称轴为 $x=3$，
所以 $ C_{\triangle PAB}=AB+AP+PB=AB+AP+PC$，
所以当 $A,P,C$ 三点共线时，$\triangle PAB$ 的周长最小．
设直线 $AC$ 的解析式为 $y=kx+b$，
把 $A\left(0,4\right),C\left(5,0\right)$ 代入解析式，
得 ${\begin{cases}
b=4,\\
5k+b=0,\\
\end{cases}} $ 解得 ${\begin{cases}k=-\dfrac{4}{5},\\
b=4.\\
\end{cases}} $
所以 $ y=-\dfrac{4}{5}x+4$，
显然点 $P$ 的横坐标为 $3$，
所以点 $P$ 的坐标为 $\left(3, \dfrac{8}{5} \right)$ 时，$\triangle PAB$ 的周长最小． -
连接 $AC$，在直线 $AC$ 下方的抛物线上，是否存在一点 $N$，使 $\triangle NAC$ 的面积最大？若存在，请求出点 $N$ 的坐标；若不存在，请说明理由．标注答案点 $N$ 坐标为 $\left( \dfrac{5}{2} , - 3 \right)$ 时，$\triangle NAC$ 的面积最大解析根据已知条件可设抛物线的解析式为 $y=a\left(x-1\right)\left(x-5\right)$，
把点 $A\left(0,4\right)$ 代入上式，解得 $a = \dfrac{4}{5}$，
所以 $y=\dfrac{4}{5}\left(x-1\right)\left(x-5\right)=\dfrac{4}{5}{x^2}-\dfrac{24}{5}x+4=\dfrac{4}{5}{\left(x-3\right)^2}-\dfrac{16}{5}$．
在直线 $AC$ 下方的抛物线上存在点 $N$，使 $\triangle NAC$ 面积最大．
设点 $N$ 的横坐标为 $t$，则 $0< t <5$，此时点 $N\left(t,\dfrac{4}{5}{t^2} - \dfrac{24}{5}t + 4\right)$．
如图，过点 $N$ 作 $y$ 轴的平行线，分别交 $x$ 轴、$AC$ 于点 $F,G$，过点 $A$ 作 $AD\perp NG$，垂足为点 $D$．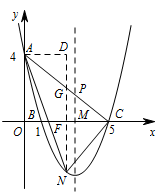
由 $(1)$ 可知直线 $AC$ 的解析式为 $y=-\dfrac{4}{5}x+4$，
把 $x=t$ 代入解析式，得 $y=-\dfrac{4}{5}t+4$，
则点 $G\left(t,-\dfrac{4}{5}t+4\right)$，
此时 $NG=-\dfrac{4}{5}t+4-\left(\dfrac{4}{5}{t^2}-\dfrac{24}{5}t+4\right)=-\dfrac{4}{5}{t^2}+4t$．
所以
$\begin{split}S_{\triangle NAC}&=S_{\triangle ANG}+S_{\triangle CGN}
\\&= \dfrac{1}{2} NG\cdot AD+ \dfrac{1}{2} NG\cdot CF
\\&= \dfrac{1}{2} NG\cdot OC
\\&= \dfrac{1}{2} \times \left( - \dfrac{4}{5}{t^2} + 4t\right) \times 5
\\&= - 2{t^2} + 10t
\\& = - 2{\left(t - \dfrac{5}{2}\right)^2} + \dfrac{25}{2}.\end{split}$
故当 $t = \dfrac{5}{2}$ 时，$\triangle NAC$ 面积取最大值 $\dfrac{25}{2}$．
由 $t = \dfrac{5}{2}$，得 $y = \dfrac{4}{5}{t^2} - \dfrac{24}{5}t + 4 = - 3$，
所以点 $N$ 坐标为 $\left( \dfrac{5}{2} , - 3 \right)$ 时，$\triangle NAC$ 的面积最大．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
