在 $ \triangle ABC $ 中，$ AB=AC $，$ \angle A=60^\circ $，点 $D$ 是线段 $BC$ 的中点，$\angle EDF=120^\circ $，$DE$ 与线段 $AB$ 相交于点 $E$，$DF$ 与线段 $AC$（或 $AC$ 的延长线）相交于点 $F$．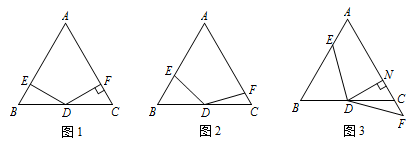
【难度】
【出处】
无
【标注】
-
如图 1，若 $ DF\perp AC $，垂足为 $ F $，$ AB=4 $，求 $ BE $ 的长；标注答案$BE=1$解析由四边形 $AEDF$ 的内角和为 $360^\circ $，可知 $DE\perp AB$，
故 $BE =\dfrac 12BD=\dfrac 14AB= 1$． -
如图 2，将 $(1)$ 中的 $\angle EDF$ 绕点 $D$ 顺时针旋转一定的角度，$DF$ 仍与线段 $AC$ 相交于点 $F$．求证：$BE + { CF } = \dfrac{1}{2}AB$；标注答案略解析取 $AB$ 的中点 $G$，连接 $DG$．
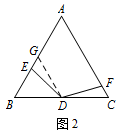则 $DG$ 为 $\triangle ABC$ 的中位线，
$\therefore DG=DC$，$\angle BGD = \angle C = 60^\circ $．
又四边形 $AEDF$ 的对角互补，
$\therefore \angle GED = \angle DFC$，
$\therefore \triangle DEG\cong \triangle DFC$，
$\therefore EG=CF$．
$\therefore BE+CF=BE+EG=BG= \dfrac{1}{2} AB$． -
如图 3，将 $(2)$ 中的 $\angle EDF$ 继续绕点 $D$ 顺时针旋转一定的角度，使 $DF$ 与线段 $AC$ 的延长线交于点 $F$，作 $DN\perp AC$ 于点 $N$，若 $DN=FN$，求证：$BE + CF = \sqrt 3\left(BE - CF\right)$．标注答案略解析取 $AB$ 的中点 $G$，连接 $DG$．
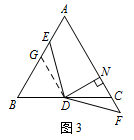由第2问知 $\triangle DEG\cong \triangle DFC$，
故 $EG=CF$．
故 $BE-CF=BE-EG=BG= \dfrac{1}{2}AB$．
设 $CN=x$，在 $\mathrm {Rt}\triangle DCN$ 中，$CD=2x$，$DN= \sqrt 3 x$．
在 $\mathrm {Rt}\triangle DFN$ 中，$NF=DN= \sqrt 3 x$，故 $EG=CF= \left(\sqrt 3 - 1\right)x$．
$BE=BG+EG=DC+CF=2x+ \left(\sqrt 3 - 1\right)x = \left(\sqrt 3 + 1\right)x$，
故 $BE+CF= \left(\sqrt 3 + 1\right)x + \left(\sqrt 3 - 1\right)x = 2\sqrt 3 x $．
$ \sqrt 3 \left(BE - CF\right) = \sqrt 3 \left[\left(\sqrt 3 + 1\right)x - \left(\sqrt 3 - 1\right)x\right] = 2\sqrt 3 x$．
故 $BE + CF = \sqrt 3 \left(BE - CF\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
