面直角坐标系 $xOy$ 中，$O$ 为坐标原点，线段 $AB$ 的两个端点 $A(0,2)$，$B(1,0)$ 分别在 $y$ 轴和 $x$ 轴的正半轴上，点 $C$ 为线段 $AB$ 的中点，现将线段 $BA$ 绕点 $B$ 按顺时针方向旋转 $90^\circ$ 得到线段 $BD$，抛物线 $y=ax^2+bx+c$（$a\ne 0$）经过点 $D$．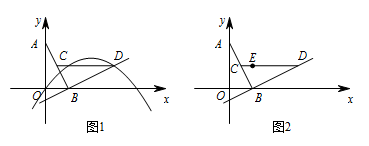
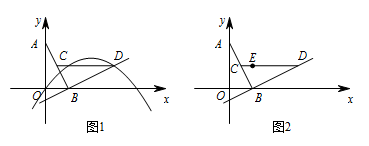
【难度】
【出处】
无
【标注】
-
如图1，若该抛物线经过原点 $O$，且 $a=-\dfrac 13$．
$(1)$ 求点 $D$ 的坐标及该抛物线的解析式．
$(2)$ 连接 $CD$，问：在抛物线上是否存在点 $P$，使得 $\angle POB$ 与 $\angle BCD$ 互余？若存在，请求出所有满足条件的点 $P$ 的坐标，若不存在，请说明理由．标注答案$(1)$ $y=-\dfrac 13x^2+\dfrac 43$；
$(2)$ 点 $P$ 的坐标是 $(\dfrac 52,\dfrac 54)$，$\left(\dfrac {11}{2},-\dfrac {11}{4}\right)$解析$(1)$ 过点 $D$ 作 $DF\perp x$ 轴于点 $F$，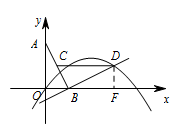
因为 $\angle DBF+\angle ABO=90^\circ$ $\angle BAO+\angle ABO=90^\circ$，
所以 $\angle DBF=\angle BAO$．
又因为 $\angle AOB=\angle BFD=90^\circ$，$AB=BD$，
所以 $\triangle AOB\cong \triangle BFD$，
所以 $DF=BO=1$，$BF=AO=2$，
所以 $D$ 点的坐标是 $(3,1)$．
根据题意得 $a=-\dfrac 13,c=0$，且 $a\times 3^2+3b+c=1$，
所以 $b=\dfrac 43$，
所以该抛物线的解析式为 $y=-\dfrac 13x^2+\dfrac 43$．
$(2)$ 因为 $C,D$ 两点的纵坐标都为 $1$，
所以 $CD\parallel x$ 轴，所以 $\angle BCD=\angle ABO$，
所以 $\angle BAO$ 与 $\angle BCD$ 互余．
若要使得 $\angle POB$ 与 $\angle BCD$ 互余，则需要满足 $\angle POB=\angle BAO$．
设点 $P$ 的坐标为 $\left(x,-\dfrac 13x^2+\dfrac 43x\right)$，
当点 $P$ 在 $x$ 轴的上方时，过点 $P$ 作 $PG\perp x$ 轴于点 $G$，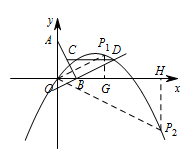
则 $\tan\angle POB=\tan\angle BAO$，即 $\dfrac{-\dfrac 13x^2+\dfrac 43x}{x}=\dfrac 12$，
所以点 $P$ 坐标为 $(\dfrac 52,\dfrac 54)$．
当点 $P$ 在 $x$ 轴的下方时，过点 $P$ 作 $PH\perp x$ 轴于点 $H$，
则 $\dfrac{\dfrac 13x^2-\dfrac 43x}{x}=\dfrac 12$，
所以点 $P$ 坐标为 $\left(\dfrac {11}{2},-\dfrac {11}{4}\right)$，
所以点 $P$ 的坐标是 $(\dfrac 52,\dfrac 54)$，$\left(\dfrac {11}{2},-\dfrac {11}{4}\right)$． -
如图2，若该抛物线 $y=ax^2+bx+c$（$a\ne 0$）经过点 $E(1,1)$，点 $Q$ 在抛物线上，且满足 $\angle QOB$ 与 $\angle BCD$ 互余，若符合条件的 $Q$ 点的个数是 $4$ 个，请直接写出 $a$ 的取值范围．标注答案$a$ 的取值范围是 $a<-\dfrac 13$ 或 $a>\dfrac{4+\sqrt{15}}{4}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
