如图 1，在 $\mathrm {Rt}\triangle ABC$ 中，$\angle B=90^\circ$，$BC=2AB=8$，点 $D,E$ 分别是边 $BC,AC$ 的中点，连接 $DE$．将 $\triangle EDC$ 绕点 $C$ 按顺时针方向旋转，记旋转角为 $\alpha$．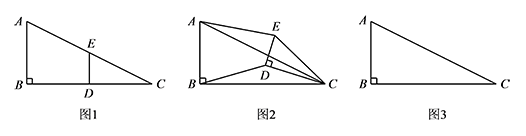
【难度】
【出处】
无
【标注】
-
问题发现
$(1)$ 当 $\alpha=0^\circ$ 时，$\dfrac{AE}{BD}=$
$(2)$ 当 $\alpha=180^\circ$ 时，$\dfrac{AE}{BD}=$ -
拓展探究
试判断：当 $0^\circ\leqslant \alpha<360^\circ$ 时，$\dfrac{AE}{BD}$ 的大小有无变化？请仅就图 2 的情形给出证明．标注答案无变化解析因为在图 1 中 $DE$ 是 $\triangle ABC$ 的中位线，
所以 $DE\parallel AB$．
所以 $\dfrac{CE}{CA}=\dfrac{CD}{CB}$，$\angle EDC=\angle B=90^\circ$．
因为在图 2中 $\triangle EDC$ 在旋转过程中形状大小不变，
所以 $\dfrac{CE}{CA}=\dfrac{CD}{CB}$ 仍然成立．
因为 $\angle ACE=\angle BCD=\alpha$，
所以 $\triangle ACE\backsim \triangle BCD$．
所以 $\dfrac{AE}{BD}=\dfrac{AC}{BC}$．
在 $\mathrm {Rt}\triangle ABC$ 中，$AC=\sqrt{AB^2+BC^2}=\sqrt{4^2+8^2}=4\sqrt 5$．
所以 $\dfrac{AC}{BC}=\dfrac{4\sqrt 5}8=\dfrac{\sqrt 5}2$．
所以 $\dfrac{AE}{BD}=\dfrac{\sqrt 5}2$．
所以 $\dfrac{AE}{BD}$ 的大小不变． -
问题解决
当 $\triangle EDC$ 旋转至 $A$，$D$，$E$ 三点共线时，直接写出线段 $BD$ 的长．标注答案$4\sqrt 5$ 或 $\dfrac{12\sqrt 5}5$解析① 当 $\triangle EDC$ 在 $BC$ 上方，且 $A,D,E$ 三点共线时，四边形 $ABCD$ 为矩形．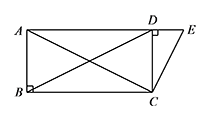
所以 $BD=AC=4\sqrt 5$；
② 当 $\triangle EDC$ 在 $BC$ 下方，且 $A,E,D$ 三点共线时，$\triangle ADC$ 为直角三角形．
由勾股定理可求得 $AD=8$，
所以 $AE=6$．
根据 $\dfrac{AE}{BD}=\dfrac{\sqrt 5}2$，
可求得 $BD=\dfrac{12\sqrt 5}5$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
