已知二次函数 $y={x^2}+bx-4$ 的图象与 $y$ 轴的交点为 $C$，与 $x$ 轴正半轴的交点为 $A$．且 $\tan \angle ACO = \dfrac{1}{4}$．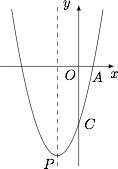
【难度】
【出处】
无
【标注】
-
$P$ 为二次函数图象的顶点，$Q$ 为其对称轴上的一点，$QC$ 平分 $\angle PQO$，求 $Q$ 点坐标；标注答案$Q$ 点坐标是 $\left(-\dfrac 32, \dfrac{\sqrt {55}}{2}\right)$ 或 $\left(-\dfrac 32, -\dfrac{\sqrt {55}}{2}\right)$解析令 $x=0$，得 $y=-4$，
所以点 $C$ 的坐标为 $\left(0,4\right)$．
而 $\tan \angle ACO=\dfrac {OA}{OC}=\dfrac 14$，
所以 $OA=1$，
所以点 $A$ 的坐标为 $\left(1,0\right)$，
将点 $A$ 坐标代入二次函数解析，得 $b=3$，
所以二次函数的解析式为 $y=x^2+3x-4$，对称轴为 $x=-\dfrac 32$．
如图．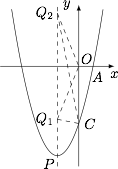
因为 $ Q$ 为抛物线对称轴上的一点，
所以设点 $Q$ 的坐标为 $\left(-\dfrac 32,n\right)$，
因为抛物线的对称轴平行于 $y$ 轴，
所以 $ \angle CQP=\angle OCQ$．
因为 $\angle OQC=\angle CQP$，
所以 $\angle OQC=\angle OCQ$，
所以 $ OQ=OC$，
所以 $ \sqrt{\left(-\dfrac 32\right)^2+n^2}=4$，
所以 $n^2+\dfrac 94=16$．
解得 $n=\pm \dfrac{\sqrt {55}}{2}$．
所以 $Q$ 点坐标是 $\left(-\dfrac 32, \dfrac{\sqrt {55}}{2}\right)$ 或 $\left(-\dfrac 32, -\dfrac{\sqrt {55}}{2}\right)$． -
是否存在实数，当 ${x_1} \leqslant x \leqslant {x_2}$ 时，$y$ 的取值范围为 $\dfrac{12}{x_2} \leqslant y \leqslant \dfrac{12}{x_1}$．若存在，求出 $x_{1}$，$x_{2}$ 的值；若不存在，说明理由．标注答案存在，当 $x_1=-3$，$x_2=-2$，$y$ 的取值范围为 $\dfrac{12}{x_2} \leqslant y \leqslant \dfrac{12}{x_1}$解析由已知可得顶点坐标为 $(-\dfrac 32,-\dfrac{25}{4})$，
① 当 $x_1\leqslant x_2< -\dfrac 32$ 时，二次函数 $y=x^2+3x-4$ 随着 $x$ 的增大而减小，
因为 $y$ 的取值范围为 $\dfrac{12}{x_2}\leqslant y\leqslant \dfrac{12}{x_1}$，
所以 $\begin{cases}x_1^2+3x_1-4=\dfrac {12}{x_1}\quad&(a)\\x_2^2+3x_2-4=\dfrac {12}{x_2}\quad&(b)\end{cases}$
由 $(a)$ 可得 $x_1=-3,-2,2$，
由 $(b)$ 可得 $x_2=-3,-2,2$，
因为 $x_1\leqslant x_2\leqslant -\dfrac 32$，
所以 $\begin{cases}x_1=-3,\\x_2=-2.\end{cases}$
② 当 $x_1\leqslant -\dfrac 32\leqslant x_2$ 时，
i）当 $-\dfrac 32-x_1\geqslant x_2-\left(-\dfrac 32\right)$ 时，
可得 $x_1+x_2\leqslant -3$，
因为 $ y$ 的取值范围为 $\dfrac{12}{x_2}\leqslant y\leqslant \dfrac{12}{x_1}$，
所以 $\begin{cases} \dfrac{4\times 1\times \left(-4\right)-3^2}{4\times 1}=\dfrac {12}{x_2}\cdots \left(1\right),\\x_1^2+3x_1-4=\dfrac {12}{x_1}\cdots \left(2\right)\end{cases}$
由 $(1)$，可得 $x_2=-\dfrac {48}{25}$，
由 $(2)$，可得 $x_1=-3$，$ -2 $，$ 2 $，
因为 $ x_1\leqslant -\dfrac 32\leqslant x_2$，$-\dfrac 32>-\dfrac{48}{25}$，
所以没有满足题意的 $x_1$，$x_2$．
ii）当 $-\dfrac 32-x_1< x_2-\left(-\dfrac 32\right)$ 时，
可得 $x_1+x_2>-3$，
因为 $ y$ 的取值范围为 $\dfrac{12}{x_2}\leqslant y\leqslant \dfrac{12}{x_1}$，
所以 $\begin{cases} \dfrac{4\times 1\times \left(-4\right)-3^2}{4\times 1}=\dfrac {12}{x_2},\\x_2^2+3x_2-4=\dfrac {12}{x_1}.\end{cases}$
解得 $\begin{cases}x_1=-\dfrac{1875}{949},\\x_2=-\dfrac {48}{25}.\end{cases}$
因为 $x_1+x_2=-\dfrac{1875}{949}-\dfrac{48}{25}\approx -1.98-1.92=-3.9<-3$，
所以没有满足题意的 $x_1$，$x_2$．
③ 当 $-\dfrac 32<x_1 \leqslant x_2$ 时，二次函数 $y=x^2+3x-4$ 随着 $x$ 的增大而增大，
因为 $ y$ 的取值范围为 $\dfrac{12}{x_2}\leqslant y\leqslant \dfrac{12}{x_1}$，
所以 $\begin{cases}x_1^2+3x_1-4=\dfrac {12}{x_2}\cdots \left(1\right),\\x_2^2+3x_2-4=\dfrac {12}{x_1}\cdots \left(2\right).\end{cases}$
$ \left(1\right)\times x_2-\left(2\right)\times x_1 $，可得
$\left(x_1-x_2\right)\left(x_1x_2+4\right)=0$，
因为 $x_1-x_2\ne 0$，
所以 $x_1x_2+4=0$，
所以 $ x_2=-\dfrac{4}{x_1}\cdots \left(3\right)$
把 $(3)$ 代入 $(1)$，可得 $x_1=-3\pm \sqrt {13}$，
因为 $ x_1>-\dfrac 32$，
所以 $ x_1=\sqrt{13}-3$，
所以 $ x_2=\dfrac{-4}{x_1}=-\sqrt {13}{-3}$，
因为 $ -\sqrt {13}{-3}<-\dfrac 32$，
所以没有满足题意的 $x_1$，$x_2$．
综上可得：$x_1=-3$，$x_2=-2$，$y$ 的取值范围为 $\dfrac{12}{x_2} \leqslant y \leqslant \dfrac{12}{x_1}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
