如图，在平面直角坐标系中，点 $O$ 为坐标原点，直线 $y=kx+1\left(k\neq 0\right)$ 与 $x$ 轴交于点 $A$，与 $y$ 轴交于点 $C$，过点 $C$ 的抛物线 $y=ax^2-\left(6a-2\right)x+b\left(a\neq 0\right)$ 与直线 $AC$ 交于另一点 $B$，点 $B$ 坐标为 $\left(4,3\right)$．
【难度】
【出处】
无
【标注】
-
点 $P$ 是射线 $CB$ 上的一个动点，过点 $P$ 作 $PQ\perp x$ 轴，垂足为点 $Q$，在 $x$ 轴上点 $Q$ 的右侧取点 $M$，使 $MQ=\dfrac 58$，在 $QP$ 的延长线上取点 $N$，连接 $PM,AN$，已知 $ \tan \angle NAQ-\tan \angle MPQ=\dfrac 12 $，求线段 $PN$ 的长；标注答案$PN=\dfrac 54$解析当 $x=0$ 时，由 $y=kx+1$ 得 $y=1$．
所以点 $C$ 的坐标为 $\left(0,1\right)$．
因为抛物线 $y=ax^2-\left(6a-2\right)x+b$，经过 $C\left(0,1\right),B\left(4,3\right)$，
所以 $\begin{cases}b=1,\\ 3=a\times 4^2-\left(6a-2\right)\times 4+b,\end{cases}$ 解得 $\begin{cases}a=\dfrac 34,\\ b=1.\end{cases}$
所以抛物线的解析式为 $y=\dfrac 34x^2-\dfrac 52x+1$．
把 $B\left(4,3\right)$ 代入 $y=kx+1$ 中，得 $k=\dfrac 12$，
所以直线 $CB$ 的解析式为 $y=\dfrac 12x+1$，点 $A$ 的坐标为 $(-2,0)$．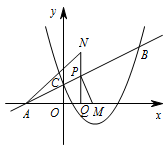
如图，显然 $\dfrac{PQ}{QA}=\dfrac{CO}{OA}=\dfrac 12$．
若设 $PQ=m$，则 $QA=2m$．
因为 $\tan\angle NAQ-\tan\angle MPQ=\dfrac 12$，
所以 $\dfrac{NQ}{QA}-\dfrac{MQ}{PQ}=\dfrac 12$，
所以 $\dfrac{PN+m}{2m}-\dfrac{\dfrac 58}{m}=\dfrac 12$，
所以 $PN=\dfrac 54$． -
在 $(1)$ 的条件下，过点 $C$ 作 $CD\perp AB$，使点 $D$ 在直线 $AB$ 下方，且 $CD=AC$，连接 $PD,NC$，当以 $PN,PD,NC$ 的长为三边长构成的三角形面积是 $\dfrac{25}{8} $ 时，在 $y$ 轴左侧的抛物线上是否存在点 $E$，连接 $NE,PE$，使得 $\triangle ENP$ 与以 $PN,PD,NC$ 的长为三边长的三角形全等？若存在，求出点 $E$ 坐标；若不存在，请说明理由．标注答案存在满足条件点 $E$，其坐标为 $\left(-1,\dfrac{17}{4}\right)$解析在 $y$ 轴左侧抛物线上存在点 $E$，使得 $\triangle ENP$ 与以 $PN,PD,NC$ 的长为三边长的三角形全等．
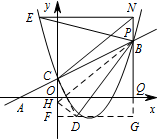如图，过点 $D$ 作 $DF\perp y$ 轴于点 $F$．
因为 $ DF\perp CF$，$CD\perp AB$，
所以 $ \angle CDF+\angle DCF=90^\circ$，$\angle DCF+\angle ACO=90^\circ$，
所以 $\angle CDF=\angle ACO$．
因为 $ CO\perp x$ 轴，$DF\perp CO$，
所以 $\angle AOC=\angle CFD=90^\circ$．
因为 $CA=CD$，
所以 $\triangle ACO\cong\triangle CDF$，
所以 $ CF=AO=2$，$DF=CO=1$，
所以 $ OF=CF-CO=1$．
在 $CF$ 上截取 $CH=PN$，连接 $DH,PH$．
因为 $ CH=PN=\dfrac 54$，
所以 $ HF=CF-CH=\dfrac 34$，
所以 $DH=\sqrt{DF^2+HF^2}=\dfrac 54$，
所以 $ DH=PN$．
因为 $ CH=PN$，$CH\parallel PN$，
所以四边形 $CHPN$ 是平行四边形，
所以 $CN=HP$，
所以 $\triangle PHD$ 是以 $PN,PD,NC$ 的长为三边长的三角形，
所以 $S_{\triangle PHD}=\dfrac{25}{8}$．
如图，延长 $FD,PQ$ 交于点 $G$．
因为 $PQ\parallel y$ 轴，
所以 $\angle G=180^\circ-\angle CFD=90^\circ$，
所以 $S_{四边形HFGP}=S_{\triangle HFD}+S_{\triangle PHD}+S_{\triangle PDG}$，
所以 $\dfrac 12\left(HF+PG\right)FG=\dfrac 12HF\cdot FD+\dfrac{25}{8}+\dfrac 12DG\cdot PG$．
因为点 $P$ 在 $y=\dfrac 12x+1$ 上，
所以设 $P\left(t,\dfrac 12t+1\right)$，
所以 $\dfrac 12\left(\dfrac 34+\dfrac 12t+1+1\right)t=\dfrac 12\times \dfrac 34\times 1+\dfrac{25}{8}+\dfrac 12\left(t-1\right)\left(\dfrac 12t+1+1\right)$，
所以 $ t=4$，
所以 $ P\left(4,3\right)$，
所以 $N\left(4,\dfrac{17}{4}\right)$，$\tan\angle DPG=\dfrac{DG}{PG}=\dfrac 34$．
因为 $\tan\angle HDF=\dfrac{HF}{FD}=\dfrac 34$，
所以 $\angle DPG=\angle HDF$．
因为 $\angle DPG+\angle PDG=90^\circ$，
所以 $\angle HDF+\angle PDG=90^\circ$，
所以 $\angle HDP=90^\circ$．
因为 $ PN=DH$，若 $\triangle ENP$ 与 $\triangle PDH$ 全等，则有两种情况．
① 当 $\angle ENP=\angle PDH=90^\circ$，$EN=PD$ 时，
因为 $PD=\sqrt{PG^2+DG^2}=5$，
所以 $EN=5$，
所以 $E\left(-1,\dfrac{17}{4}\right)$，由 $(1)$ 得抛物线 $y=\dfrac 34x^2-\dfrac 52x+1$，
当 $x=-1$ 时，$y=\dfrac{17}{4}$，
所以点 $E$ 在此抛物线上．
② 当 $\angle NPE=\angle HDP=90^\circ$，$BE=PD$ 时，则 $E\left(-1,3\right)$，但点 $E$ 不在抛物线上．
综上可得，存在满足条件点 $E$，其坐标为 $\left(-1,\dfrac{17}{4}\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
