已知抛物线 $y=ax^2+bx+c$ 的顶点为 $\left(1,0\right)$,与 $y$ 轴的交点坐标为 $\left(0,\dfrac14\right)$,$R\left(1,1\right)$ 是抛物线对称轴 $l$ 上的一点.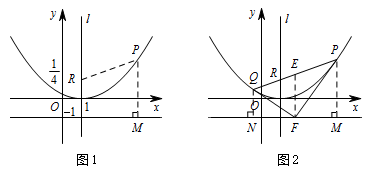

【难度】
【出处】
无
【标注】
-
若 $P$ 是抛物线上的一个动点(如图1),求证:点 $P$ 到 $R$ 的距离与点 $P$ 到直线 $y=-1$ 的距离恒相等;标注答案略解析由题意可设抛物线解析式为 $y=a\left(x-1\right)^2$,
把 $\left(0, \dfrac14\right)$ 代入得 $a=\dfrac14 $,
所以抛物线解析式为 $y=\dfrac14 \left(x-1\right)^2$.
如图 1,设点 $P$ 的坐标为 $\left(x,\dfrac14\left(x-1\right)^2\right)$,则 $PM=\dfrac14\left(x-1\right)^2+1$,
因为
$\begin{split} PR^2&=\left(x-1\right)^2+\left[\dfrac14\left(x-1\right)^2-1\right]^2\\&=\left(x-1\right)^2+\left[\dfrac14\left(x-1\right)\right]^4-\dfrac12\left(x-1\right)^2+1\\&=\left[\dfrac14\left(x-1\right)\right]^4+\dfrac12\left(x-1\right)^2+1\\&=\left[\dfrac14\left(x-1\right)^2+1\right]^2,\end{split}$
所以 $PR=\dfrac14\left(x-1\right)^2+1=PM$,
即点 $P$ 到 $R$ 的距离与点 $P$ 到直线 $y=-1$ 的距离恒相等. -
设直线 $PR$ 与抛物线的另一交点为 $Q$,$E$ 为线段 $PQ$ 的中点,过点 $P,E,Q$ 分别作直线 $y=-1$ 的垂线.垂足分别为 $M,F,N$(如图2).求证:$PF\perp QF$.标注答案略解析由 $(1)$ 得 $QN=QR$,$PR=PM$,
所以 $ PQ=PR+QR=PM+QN$.
因为 $EF\perp MN$,$QN\perp MN$,$PM\perp MN$,
而 $E$ 为线段 $PQ$ 的中点,
所以 $ EF$ 为梯形 $PMNQ$ 的中位线,
所以 $EF=\dfrac12\left(QN+PM\right)=\dfrac12 PQ$,
所以 $EF=EQ=EP$,
所以点 $F$ 在以 $PQ$ 为直径的圆上,
所以 $\angle PFQ=90^\circ $,即 $PF\perp QF$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2