题目 函数 $y=f(x)$ 是定义在 $\mathbb R$ 上的偶函数，且 $f(-1+x)=f(-1-x)$，当 $x\in[-2,-1]$ 时，$f(x)=t(x+2)^{2}-t(x+2)(t\in\mathbb R)$，记函数 $y=f(x)$ 的图象在 $\left(\dfrac{1}{2},f\left(\dfrac{1}{2}\right)\right)$ 处的切线为 $l$，$f'\left(\dfrac{1}{2}\right)=1$． 问题1 求 $y=f(x)$ 在 $[0,1]$ 上的解析式； 答案1 $f(x)=-4x^{3}+4x$ 解析1 因为函数 $y=f(x)$ 是定义在 $\mathbb R$ 上的偶函数，由$$\begin{cases}f(-1+x)=f(-1-x),\\f(x)=f(-x),\end{cases}$$得$$f(-1+x)=f(-1-x)=f(1+x),$$所以 $y=f(x)$ 是周期为 $2$ 的函数．<br/>因为当 $x\in[0,1]$ 时，$x-2\in[-2,-1]$，所以$$f(x)=f(x-2)=tx^{3}-tx.$$由 $f'\left(\dfrac{1}{2}\right)=1$ 可知$$t=-4,$$所以$$f(x)=f(x-2)=-4x^{3}+4x.$$ 备注1 问题2 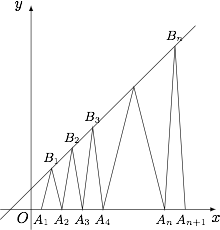点列 $B_{1}(b_{1},2)$，$B_{2}(b_{2},3)$，$\cdots$，$B(b_{n},n+1)$ 在 $l$ 上，$A_{1}(x_{1},0)$，$A_{2}(x_{2},0)$，$\cdots$，$A_{n}(x_{n},0)$ 依次为 $x$ 轴上的点，如图，当 $n\in\mathbb N^{*}$ 时，点 $A_{n},B_{n},A_{n+1}$ 构成以 $A_{n}A_{n+1}$ 为底边的等腰三角形．若 $x_{1}=a(0<a<1)$，求数列 $\{x_{n}\}$ 的通项公式；<img src="/static/images/40ead0df8f55a1698d6b8979d04b5f9e.png" class="img-responsive" /> 答案2 $x_{n}=\begin{cases}n-1+a,&n=1,3,5,\cdots\\n-a,&n=2,4,6,\cdots\end{cases}$ 解析2 因为函数 $y=f(x)$ 的图象在 $\left(\dfrac{1}{2},f\left(\dfrac{1}{2}\right)\right)$ 处的切线为 $l$，且 $f'\left(\dfrac{1}{2}\right)=1$，所以切线 $l$ 过点 $\left(\dfrac{1}{2},\dfrac{3}{2}\right)$ 且斜率为 $1$，故切线 $l$ 的方程为$$y=x+1.$$因为 $B_{1}(b_{1},2)$，$B_{2}(b_{2},3)$，$B_{n}(b_{n},n+1)$ 在 $l$ 上，有 $n+1=b_{n}+1$，即$$b_{n}=n.$$因为点 $A_{n},B_{n},A_{n+1}$ 构成以 $A_{n}A_{n+1}$ 为底边的等腰三角形，所以\[x_{n}+x_{n+1}=2b_{n}=2n,\]同理\[x_{n+1}+x_{n+2}=2n+2,\]两式相减得$$x_{n+2}-x_{n}=2,$$因为 $x_{1}=a,x_{2}=2-a$，所以$$x_{n}=\begin{cases}n-1+a,&n=1,3,5,\cdots\\n-a,&n=2,4,6,\cdots\end{cases}$$ 备注2 问题3 在 $(2)$ 的条件下，是否存在实数 $a$ 使得数列 $\{x_{n}\}$ 是等差数列？如果存在，求出 $a$ 的一个值；如果不存在，请说明理由． 答案3 存在，$a=\dfrac 12$ 解析3 假设 $\{x_{n}\}$ 是等差数列，则$$-a=-1+a,$$所以$$a=\dfrac{1}{2},$$故存在实数 $a=\dfrac 12$ 使得数列 $\{x_{n}\}$ 是等差数列． 备注3