如图,直线 $l\perp AB$ 于点 $B$,点 $C$ 在 $AB$ 上,且 $AC:CB=2:1$,点 $M$ 是直线上的动点,作点 $B$ 关于直线 $CM$ 的对称点 $B'$,直线 $AB'$ 与直线 $CM$ 相交于点 $P$,连接 $PB$.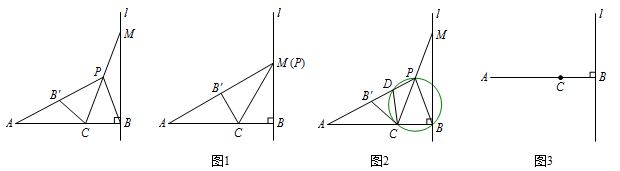

【难度】
【出处】
无
【标注】
-
如图1,若点 $P$ 与点 $M$ 重合,则 $\angle PAB=$
-
如图2,若点 $P$ 与点 $M$ 不重合,设过 $P,B,C$ 三点的圆与直线 $AP$ 相交于点 $D$,连接 $CD$.求证:
$(1)$ $CD=CB'$;
$(2)$ $PA=2PB$.标注答案$(1)$ 由点 $B$ 与点 $B'$ 关于 $PC$ 对称,
可得 $\angle DPC=\angle B'PC=\angle BPC$,$CB'=CB$,
因为四边形 $DCPB$ 是圆内接四边形,
所以 $CD=CB=CB'$.
$(2)$ 如图,过点 $B$ 作 $BE\parallel CP$ 交 $AP$ 延长线于点 $E$.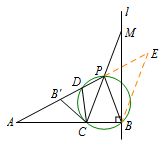 由 $(1)$ 可得 $\angle DPC=\angle BPC$,
由 $(1)$ 可得 $\angle DPC=\angle BPC$,
从而 $\angle E=\angle DPC=\angle CPB=\angle PBE$,
所以 $PB=PE$.
可得 $\dfrac{PA}{PB}=\dfrac{PA}{PE}=\dfrac{CA}{CB}=2$,
所以 $PA=2PB$解析略 -
如图3,若 $AC=2,BC=1$,则满足条件 $PA=2PB$ 的点都在一个确定的圆上.如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点 $Q$,都满足 $QA=2QB$.标注答案由阿氏圆的概念可得满足 $PA=2PB$ 的点都在一个确定的圆上.
作点 $A$ 关于 $l$ 的对称点 $D$,有 $DA=2DB$,
则该圆是以 $CD$ 为直径的 $\odot O$,则 $OA=4$,$OB=1$.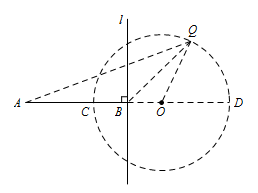 在 $\odot O$ 上任取一点 $Q$,连接 $QA,QB,QO$,则 $OQ=2$,
在 $\odot O$ 上任取一点 $Q$,连接 $QA,QB,QO$,则 $OQ=2$,
所以 $\dfrac{OA}{OQ}=\dfrac{OQ}{OB}=2$.
所以 $\triangle AOQ\sim \triangle QOB$,且相似比 $k=2$,
从而得到 $QA=2OB$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3