如图，在直角坐标系中，$\mathrm {Rt}\triangle OAB$ 的直角顶点 $A$ 在 $x$ 轴上，$OA=4$，$AB=3$．动点 $M$ 从点 $A$ 出发，以每秒 $1$ 个单位长度的速度，沿 $AO$ 向终点 $O$ 移动；同时点 $N$ 从点 $O$ 出发，以每秒 $1.25$ 个单位长度的速度，沿 $OB$ 向终点 $B$ 移动．当两个动点运动了 $x$ 秒（$0<x<4$）时，是否存在某一时刻，使 $\triangle OMN$ 是直角三角形？若存在，求出 $x$ 的值；若不存在，请说明理由．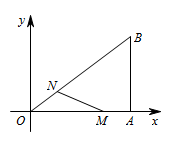
【难度】
【出处】
无
【标注】
【答案】
存在某一时刻，使 $\triangle OMN$ 是直角三角形．
理由如下：
① 如图，若 $\angle OMN=90^\circ $．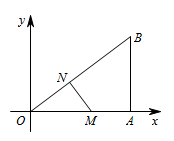
则 $MN\parallel AB$，
此时 $OM=4-x$，$ON=1.25x$，
$\because MN\parallel AB$，
$\therefore \triangle OMN\backsim \triangle OAB$，
$\therefore \dfrac{OM}{OA}=\dfrac{ON}{OB}$，
即 $\dfrac{4-x}{4}=\dfrac{1.25x}{5}$，
解得 $x=2$．
② 如图，若 $\angle ONM=90^\circ $．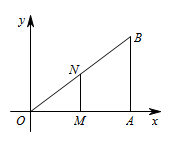
则 $\angle ONM=\angle OAB$，
此时 $OM=4-x$，$ON=1.25x$，
$\because \angle ONM=\angle OAB$，$\angle MON=\angle BOA$，
$\therefore \triangle OMN\backsim \triangle OBA$，
$\therefore \dfrac{OM}{OB}=\dfrac{ON}{OA}$，
即 $\dfrac{4-x}{5}=\dfrac{1.25x}{4}$，
解得 $x=\dfrac{64}{41}$．
综上所述，$x$ 的值是 $2$ 或 $\dfrac{64}{41}$
理由如下：
① 如图，若 $\angle OMN=90^\circ $．
则 $MN\parallel AB$，此时 $OM=4-x$，$ON=1.25x$，
$\because MN\parallel AB$，
$\therefore \triangle OMN\backsim \triangle OAB$，
$\therefore \dfrac{OM}{OA}=\dfrac{ON}{OB}$，
即 $\dfrac{4-x}{4}=\dfrac{1.25x}{5}$，
解得 $x=2$．
② 如图，若 $\angle ONM=90^\circ $．
则 $\angle ONM=\angle OAB$，此时 $OM=4-x$，$ON=1.25x$，
$\because \angle ONM=\angle OAB$，$\angle MON=\angle BOA$，
$\therefore \triangle OMN\backsim \triangle OBA$，
$\therefore \dfrac{OM}{OB}=\dfrac{ON}{OA}$，
即 $\dfrac{4-x}{5}=\dfrac{1.25x}{4}$，
解得 $x=\dfrac{64}{41}$．
综上所述，$x$ 的值是 $2$ 或 $\dfrac{64}{41}$
【解析】
略
答案
解析
备注
