如图，在平行四边形 $ABCD$ 中，$AB =6$，$BC =4$，$\angle B =60^\circ $，点 $E$ 是边 $AB$ 上的一点，点 $F$ 是边 $CD$ 上一点，将平行四边形 $ABCD$ 沿 $EF$ 折叠，得到四边形 $EFGH$，点 $A$ 的对应点为点 $H$，点 $D$ 的对应点为点 $G$．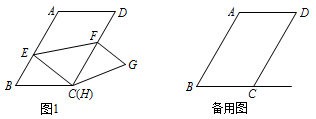
【难度】
【出处】
无
【标注】
-
当 点 $H$ 与点 $C$ 重合时．
$(1)$ 填空：点 $E$ 到 $CD$ 的距离是
$(2)$ 求证：$\triangle BCE \cong \triangle GCF$；
$(3)$ 求 $\triangle CEF$ 的面积；标注答案$(1)$ $2\sqrt3$；
$(2)$ 略；
$(3)$ $S_{\triangle CEF}=\dfrac{7\sqrt3}{2}$解析$(2)$ 因为四边形 $ABCD$ 是平行四边形，
所以 $ AD=BC$，$\angle D=\angle B$，
由折叠可知 $AD=CG$，$\angle D=\angle G$，$\angle A=\angle ECG$，
所以 $ BC=GC$，$\angle B=\angle G$，$\angle BCD=\angle ECG$，
所以 $ \angle BCE=\angle GCF$，
所以 $ \triangle BCE\cong \triangle GCF$．
$(3)$ 过点 $E$ 作 $EP\perp BC$ 于 $P$，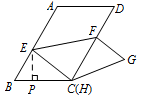
因为 $\angle B=60^\circ$，$\angle EPB=90^\circ$，
所以 $\angle BEP=30^\circ$，
所以 $ BE=2BP$．
可设 $BP=m$，则 $BE=2m$，
所以 $ EP=BE\cdot \sin {60^\circ}=2m\times\dfrac{\sqrt3}{2}=\sqrt3m$．
由折叠可知 $AE=CE$，
因为 $AB=6$，
所以 $ AE=CE=6-2m$．
因为 $ BC=4$，
所以 $ PC=4-m$．
在 $\mathrm {Rt}\triangle ECP$ 中，由勾股定理得 $\left(4-m\right)^2+\left(\sqrt3m\right)^2=\left(6-2m\right)^2$，
所以 $ m=\dfrac54$，
所以 $ EC=6-2m=6-2\times\dfrac54=\dfrac72$．
因为 $ \triangle BCE\cong\triangle GCF$，
所以 $ CF=EC=\dfrac72$，
所以 $ S_{\triangle CEF}=\dfrac12\times\dfrac72\times2\sqrt3=\dfrac{7\sqrt3}{2}$． -
当点 $H$ 落在射线 $BC$ 上，且 $CH =1$ 时，直线 $EH$ 与直线 $CD$ 交于点 $M$，请直接写出 $\triangle MEF$ 的面积．标注答案$\dfrac{124\sqrt3}{35}$ 或 $4\sqrt3$解析① 当点 $H$ 在 $BC$ 的延长线上时，过点 $E$ 作 $EQ\perp BC$ 于点 $Q$．
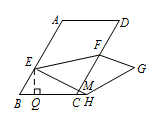因为 $\angle B=60^\circ $，$ \angle EQB=90^\circ$，
所以 $ \angle BEQ=30^\circ$．
所以 $ BE=2BQ$．
设 $BQ=n$，则 $BE=2n$，
所以 $ QE=BE\cdot \sin 60^\circ =2n\times \dfrac {\sqrt 3}{2}=\sqrt 3n$．
由折叠可知，$AE=HE$，
因为 $ AB=6$，
所以 $ AE=HE=6-2n$．
因为 $ BC=4$，$CH=1$，
所以 $ BH=5$，
所以 $ QH=5-n$．
在 $ \mathrm {Rt}\triangle EHQ $ 中，$\left(5-n\right)^2+\left(\sqrt 3n\right)^2=\left(6-2n\right)^2$，
解得 $n=\dfrac {11}{14}$．
所以 $ AE=HE=6-2n=\dfrac {31}{7}$．
因为 $ AB\parallel CD$，
所以 $ \triangle CMH\backsim \triangle BEH$，
所以 $ \dfrac {MH}{HE}=\dfrac {CH}{BH}$，
即 $\dfrac {MH}{\dfrac {31}{7}}=\dfrac {1}{5}$，
所以 $MH=\dfrac {31}{35}$，
所以 $ EM=\dfrac {31}{7}-\dfrac {31}{35}=\dfrac {124}{35}$．
所以 $ S_{\triangle EMF}=\dfrac 12\times \dfrac {124}{35}\times 2\sqrt 3=\dfrac {124\sqrt 3}{35}$．
② 当点 $H$ 在 $BC$ 上时，过点 $E$ 作 $EQ\perp BC$ 于点 $Q$．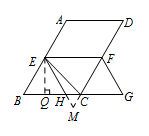
由折叠可知，$AE=HE$，
因为 $AB=6$，
所以 $AE=HE=6-2n$．
因为 $ BC=4$，$ CH=1$，
所以 $ BH=3$，$ QH=3-n$．
在 $\mathrm {Rt}\triangle EHQ$ 中，$\left(3-n\right)^2+\left(\sqrt 3n\right)^2=\left(6-2n\right)^2$，
解得 $n=\dfrac 32$．
所以 $ BE=2n=3$，$AE=HE=3$，
所以 $ BE=EH$．
因为 $ \angle B=60^\circ$，
所以 $\triangle BHE$ 是等边三角形，
所以 $ \angle BEH=60^\circ$．
因为 $ \angle AEF=\angle HEF$，
所以 $\angle FEH=\angle AEF=60^\circ$，
所以 $ EF\parallel BC$，
所以 $ DF=CF=3$．
因为 $AB\parallel CD$，
所以 $ \triangle CMH\backsim \triangle BEH$，
所以 $ \dfrac {CM}{BE}=\dfrac {CH}{BH}$，
即 $ \dfrac {CM}{3}=\dfrac {1}{3}$．
所以 $ CM=1$，
所以 $ EM=4$，
所以 $S_{\triangle EMF}=\dfrac 12\times 4\times 2\sqrt 3=4\sqrt 3$．
综上可得，$\triangle EMF$ 的面积为 $\dfrac {124\sqrt 3}{35}$ 或 $4\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
