如图，抛物线经过 $ A\left( - 2,0\right) $，$ B\left( - \dfrac{1}{2},0\right) $，$ C\left(0,2\right) $ 三点．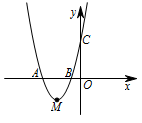
【难度】
【出处】
无
【标注】
-
在直线 $ AC $ 下方的抛物线上有一点 $ D $，使得 $ \triangle DCA $ 的面积最大，求点 $ D $ 的坐标；标注答案点 $ D $ 的坐标为 $ \left(-1,-1\right) $解析因为该抛物线过点 $ C\left(0,2\right) $，
所以可设该抛物线的解析式为 $ y = a{x^2} + bx + 2 $．
将 $ A\left(-2,0\right) $，$ B\left(-\dfrac{1}{2},0\right) $ 代入，
得 $ {\begin{cases}
4a - 2b + 2 = 0, \\
\dfrac{1}{4}a - \dfrac{1}{2}b + 2 = 0 ,\\
\end{cases}} $ 解得 $ {\begin{cases}a = 2,\\
b = 5.\\
\end{cases}} $
所以此抛物线的解析式为 $ y = 2{x^2} + 5x + 2 $．
由题意可求得直线 $ AC $ 的解析式为 $ y = x + 2 $．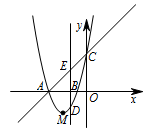
如图，设 $ D $ 点的横坐标为 $ t\left(-2<t<0\right) $，则 $ D $ 点的纵坐标为 $ 2{t^2} + 5t + 2 $．
过 $ D $ 作 $ y $ 轴的平行线交 $ AC $ 于 $ E $．
设 $ E $ 点的坐标为 $ \left(t,t+2\right) $，
所以 $ DE = t + 2 -\left(2{t^2} + 5t + 2\right)= - 2{t^2} - 4t $，用 $ h $ 表示点 $ C $ 到线段 $ DE $ 所在直线的距离，
所以 $ {S_{\triangle DAC}} = {S_{\triangle CDE}} + {S_{\triangle ADE}} = \dfrac{1}{2}DE \cdot h + \dfrac{1}{2}DE \cdot\left(2 - h\right)= \dfrac{1}{2}DE \cdot 2 = - 2{t^2} - 4t = - 2{\left(t + 1\right)^2} + 2$．
因为 $ -2<t<0 $，
所以 当 $ t=-1 $ 时，$ \triangle DAC $ 面积最大，此时点 $ D $ 的坐标为 $ \left(-1,-1\right) $． -
设点 $ M $ 是抛物线的顶点，试判断抛物线上是否存在点 $ H $ 满足 $ \angle AMH = {90^\circ } $？若存在，请求出点 $ H $ 的坐标；若不存在，请说明理由．标注答案存在，点 $ H $ 坐标为 $ \left(- \dfrac{11}{12},- \dfrac{65}{72}\right) $解析由 $(1)$ 知，点 $ M $ 的坐标为 $ \left(- \dfrac{5}{4},- \dfrac{9}{8}\right) $．
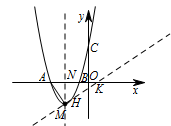如图，假设存在点 $ H $，满足 $ \angle AMH = {90^\circ } $，
作直线 $ MH $ 交 $ x $ 轴于点 $ K\left(x,0\right) $，作 $ MN\perp x $ 轴于点 $ N $．
因为 $ \angle AMN + \angle KMN = {90^\circ } $，$ \angle NKM + \angle KMN = {90^\circ } $，
所以 $\angle AMN = \angle NKM $．
因为 $\angle ANM = \angle MNK = {90^\circ } $，
所以 $\triangle ANM\backsim \triangle MNK$，
所以 $\dfrac{AN}{MN} = \dfrac{MN}{NK} $，
所以 $M{N^2} = AN \cdot NK $，
所以 ${\left(\dfrac{9}{8}\right)^2} =\left(2 - \dfrac{5}{4}\right)\left(x + \dfrac{5}{4}\right) $，
所以 $x = \dfrac{7}{16} $，
所以点 $ K $ 的坐标为 $ \left(\dfrac{7}{16},0\right) $，
所以直线 $ MK $ 的解析式为 $y = \dfrac{2}{3}x - \dfrac{7}{24}$．
所以 $\begin{cases} y=\dfrac 23x-\dfrac{7}{24}, \quad \cdots \cdots ① \\ y=2x^2+5x+2, \quad \cdots \cdots ② \end{cases} $
把 $ ① $ 代入 $ ② $，化简得 $48{x^2} + 104x + 55 = 0$，
$\Delta = {\left(104\right)^2} - 4 \times 48 \times 55 = 64 \times 4 = 256>0$，
所以 ${x_1} = - \dfrac{5}{4} $，$ {x_2} = - \dfrac{11}{12} $．
将 $ {x_2} = - \dfrac{11}{12} $ 代入 $y = \dfrac{2}{3}x - \dfrac{7}{24}$ 中，解得 $y = - \dfrac{65}{72}$．
所以直线 $ MN $ 与抛物线有两个交点（其中一点为顶点 $ M $）．
所以抛物线上必存在一点 $ H $，使 $ \angle AMH=90^\circ $，
此时点 $ H $ 坐标为 $ \left(- \dfrac{11}{12},- \dfrac{65}{72}\right) $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
