设平面内一点到等边三角形中心的距离为 $d$，等边三角形的内切圆半径为 $r$，外接圆半径为 $R$．对于一个点与等边三角形，给出如下定义：满足 $r\leqslant d\leqslant R$ 的点叫做等边三角形的中心关联点．
在平面直角坐标系 $xOy$ 中，等边 $\triangle ABC$ 的三个顶点的坐标分别为 $A(0,2)$，$B(-\sqrt 3,-1)$，$C(\sqrt 3,-1)$．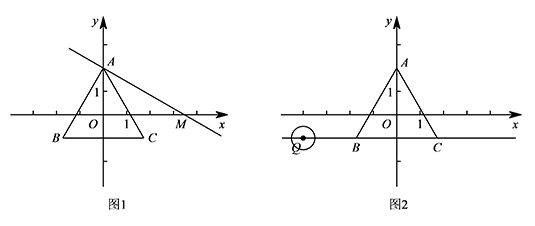
在平面直角坐标系 $xOy$ 中，等边 $\triangle ABC$ 的三个顶点的坐标分别为 $A(0,2)$，$B(-\sqrt 3,-1)$，$C(\sqrt 3,-1)$．
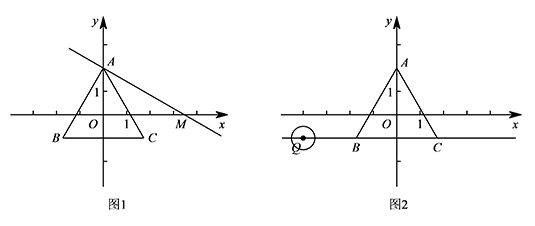
【难度】
【出处】
无
【标注】
-
已知点 $D(2,2),E(\sqrt 3,1),F\left(-\dfrac 12,-1\right)$，在点 $D,E,F$ 中，是等边 $\triangle ABC$ 的中心关联点的是
其中心为原点 $O$，内切圆半径 $r=1$，外接圆半径 $R=2$．
因为 $OD=\sqrt{2^2+2^2}=2\sqrt 2$，$OE=\sqrt{(\sqrt 3)^2+1^2}=2$，$OF=\sqrt{\left(-\dfrac 12\right)^2+(-1)^2}=\dfrac{\sqrt 5}2$，
所以 $OD>R$，$r\leqslant OE\leqslant R$，$r\leqslant OF\leqslant R$，
所以 $E,F$ 是等边 $\triangle ABC$ 的中心关联点． -
如图1．
$(1)$ 过点 $A$ 作直线交 $x$ 轴正半轴于点 $M$，使 $\angle AMO=30^\circ$．若线段 $AM$ 上存在等边 $\triangle ABC$ 的中心关联点 $P(m,n)$，求 $m$ 的取值范围；
$(2)$ 将直线 $AM$ 向下平移得到直线 $y=kx+b$，当 $b$ 满足什么条件时，直线 $y=kx+b$ 上总存在等边 $\triangle ABC$ 的中心关联点；标注答案$(1)$ $0\leqslant m\leqslant \sqrt 3$；
$(2)$ $-\dfrac{4\sqrt 3}3\leqslant b\leqslant 2$解析$(1)$ 由 $\angle AMO=30^\circ$，可得 $AM=2OA=4$，$OM=\sqrt 3OA=2\sqrt 3$．
如图，过点 $O$ 作 $OH\perp AM$．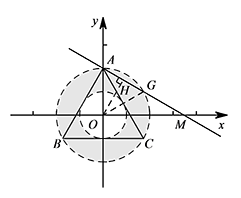
易求 $OH=\dfrac 12OM=\sqrt 3$，
即 $AM$ 与外接圆相交，与内切圆相离，记 $AM$ 与另一个交点为 $G$．
连接 $OG$，则 $\triangle OAG$ 为等边三角形，
所以 $AG=OG=\dfrac 12AM$，即点 $G$ 为 $AM$ 中点，
所以点 $G$ 坐标为 $(\sqrt 3,1)$．
显然 $AG$ 上的点都是 $\triangle ABC$ 的中心关联点，
所以 $0\leqslant m\leqslant \sqrt 3$．
$(2)$ 直线 $AM$ 向下平移的过程中，只要与 $\triangle ABC$ 的外接圆和内切圆组成的圆环有交点，则直线 $y=kx+b$ 上就存在等边 $\triangle ABC$ 的中心关联点．
如图，直线 $IJ\parallel AM$，且与 $\triangle ABC$ 的外接圆相切于点 $K$，此时为直线 $y=kx+b$ 的临界状态．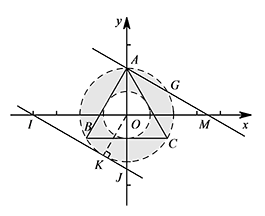
连接 $OK$，则 $OK=2$．
所以 $OJ=\dfrac{OK}{\cos 30^\circ}=\dfrac{4\sqrt 3}{3}$．
所以 $-\dfrac{4\sqrt 3}3\leqslant b\leqslant 2$． -
如图2，点 $Q$ 为直线 $y=-1$ 上一动点，$\odot Q$ 的半径为 $\dfrac 12$．当点 $Q$ 从点 $(-4,-1)$ 出发，以每秒 $1$ 个单位的速度向右移动，运动时间为 $t$ 秒，是否存在某一时刻 $t$，使得 $\odot Q$ 上所有点都是等边 $\triangle ABC$ 的中心关联点？如果存在，请直接写出所有符合题意的 $t$ 的值；如果不存在，请说明理由．标注答案存在，符合题意的 $t$ 的值为 $4-\dfrac{\sqrt 5}2$ 或 $4+\dfrac{\sqrt 5}2$解析如图，当点 $Q$ 移动到 $Q_1,Q_2$ 位置时，即 $\odot Q$ 内切于圆环时，$\odot Q$ 上所有点都是等边 $\triangle ABC$ 的中心关联点．
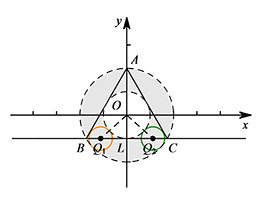连接 $OQ_1,OQ_2$，则 $OQ_1=OQ_2=\dfrac 32$．
令直线 $y=-1$ 与 $y$ 轴的交点为 $L$，则 $OL=1$．
所以 $Q_1L=Q_2L=\sqrt{\left(\dfrac 32\right)^2-1^2}=\dfrac{\sqrt 5}2$，
所以 $t_1=4-\dfrac{\sqrt 5}2$，$t_2=4+\dfrac{\sqrt 5}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
