在等边 $\triangle ABC$ 中，$E$ 为直线 $AB$ 上一点，连接 $EC$，$ED$ 与直线 $BC$ 交于点 $D$，$ED=EC$．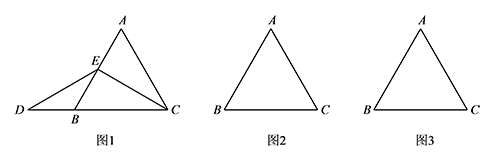
【难度】
【出处】
无
【标注】
-
如图1，$AB=1$，点 $E$ 是 $AB$ 的中点，求 $BD$ 的长；标注答案由点 $E$ 是 $AB$ 的中点，
可得 $\angle BCE=\dfrac 12\angle ACB=30^\circ$．
而 $ED=EC$，
所以 $\angle D=\angle ECD=30^\circ$，
所以 $\angle BED=\angle ABC-\angle D=30^\circ$，
从而 $BD=BE=\dfrac 12AB=\dfrac 12$解析略 -
点 $E$ 是 $AB$ 边上任意一点（不与 $AB$ 边的中点和端点重合），依题意，将图2补全，判断 $AE$ 与 $BD$ 间的数量关系并证明；标注答案
解法一 如图，将 $\triangle BED$ 沿着 $BE$ 翻折得到 $\triangle BEG$，连接 $CG$．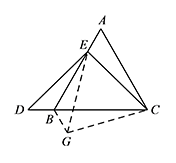
显然 $\angle EBG=\angle EBD=120^\circ$，$\angle D=\angle EGB$，$ED=EG$，$BD=BG$．
所以 $\angle CBG=\angle EBG-\angle EBC=60^\circ$．
因为 $ED=EC$，
所以 $\angle EGB=\angle D=\angle ECB$，$EG=EC$．
所以 $\angle CEG=\angle CBG=60^\circ$，即 $\triangle ECG$ 为等边三角形．
所以 $\triangle ACE\cong \triangle BCG$，
从而 $AE=BG=BD$．解法二 如图，过点 $E$ 作 $EF\parallel AC$ 交 $BC$ 于点 $F$．
由已知可得 $\triangle EBF$ 为等边三角形，
所以 $EB=EF=FB$，$AE=CF$，$\angle EBD=\angle EFC$．
因为 $ED=EC$，
所以 $\angle D=\angle ECF$，
所以 $\triangle EDB\cong \triangle ECF$，
从而 $BD=FC=AE$．解法三 如图，过点 $E$ 作 $EH\parallel BC$ 交 $AC$ 于点 $H$，连接 $BH$．
易证 $\triangle AEH$ 为等边三角形，四边形 $EBCH$ 为等腰梯形，
所以 $AE=EH$，$\angle HBC=\angle ECB$．
而 $ED=EC$，
所以 $\angle D=\angle ECB=\angle HBC$，
所以 $ED\parallel HB$，即四边形 $EDBH$ 为平行四边形，
所以 $AE=EH=BD$解析略 -
点 $E$ 不在线段 $AB$ 上，请在图3中画出符合条件的一个图形，并判断 $AE$ 与 $BD$ 间的数量关系．标注答案① 如图，将 $\triangle BED$ 沿着 $BE$ 翻折得到 $\triangle BEG$，连接 $CG$．
同上可证 $\triangle ECG$ 为等边三角形，
从而 $\triangle CAE\cong \triangle CBG$，
所以 $AE=BG=BD$；
② 如图，将 $\triangle BED$ 沿着 $BE$ 翻折得到 $\triangle BEG$，连接 $CG$．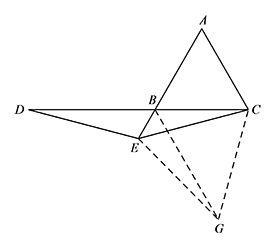
易证 $\triangle ECG$ 为等边三角形，
从而 $\triangle CAE\cong \triangle CBG$，
所以 $AE=BG=BD$．
综上可得，当点 $E$ 在直线 $AB$ 上时，均有 $AE=BD$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
