已知抛物线的解析式为 $y=-\dfrac{1}{20}x^2+\dfrac{1}{10}x+5$，与 $x$ 轴交于点 $C$，抛物线的对称轴与 $x$ 轴交于点 $B$，点 $A(2,5)$ 为该抛物线上一点，在抛物线上是否存在一点 $P$，使得 $\angle PAB=\angle ABC$？若存在，求出点 $P$ 的坐标，若不存在，请说明理由．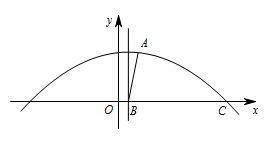
【难度】
【出处】
无
【标注】
【答案】
作线段 $AB$ 的垂直平分线，与抛物线交于两点，此时 $\angle PAB=\angle ABC$，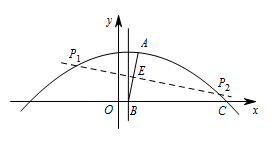
抛物线的对称轴是直线 $x=1$，则 $B(1,0)$，
因为 $A(2,5)$，
所以直线 $AB$ 表达式为 $y=5x-5$，$E(1.5,2.5)$，
所以直线 $P_1P_2$ 表达式为 $k=-\dfrac 15$，
设直线 $P_1P_2$ 表达式为 $y=-\dfrac 15x+b$，
把 $E(1.5,2.5)$ 代入表达式得 $b=2.8$，
直线 $P_1P_2$ 表达式为 $y=-\dfrac 15x+2.8$，
由题意得 $\begin{cases}y=-\dfrac 15x+2.8,\\ y=-\dfrac{1}{20}x^2+\dfrac {1}{10}x+5.\end{cases}$
解得 $\begin{cases}x_1=3+\sqrt{53},\\ y_1=\dfrac {11}{5}-\dfrac{\sqrt{53}}{5}.\end{cases}$
$\begin{cases}x_2=3-\sqrt{53},\\ y_2=\dfrac {11}{5}+\dfrac{\sqrt{53}}{5}.\end{cases}$
所以 $P_1(3+\sqrt{53},\dfrac {11}{5}-\dfrac{\sqrt{53}}{5})$，$P_2(3-\sqrt{53},\dfrac {11}{5}+\dfrac{\sqrt{53}}{5}))$
抛物线的对称轴是直线 $x=1$，则 $B(1,0)$，因为 $A(2,5)$，
所以直线 $AB$ 表达式为 $y=5x-5$，$E(1.5,2.5)$，
所以直线 $P_1P_2$ 表达式为 $k=-\dfrac 15$，
设直线 $P_1P_2$ 表达式为 $y=-\dfrac 15x+b$，
把 $E(1.5,2.5)$ 代入表达式得 $b=2.8$，
直线 $P_1P_2$ 表达式为 $y=-\dfrac 15x+2.8$，
由题意得 $\begin{cases}y=-\dfrac 15x+2.8,\\ y=-\dfrac{1}{20}x^2+\dfrac {1}{10}x+5.\end{cases}$
解得 $\begin{cases}x_1=3+\sqrt{53},\\ y_1=\dfrac {11}{5}-\dfrac{\sqrt{53}}{5}.\end{cases}$
$\begin{cases}x_2=3-\sqrt{53},\\ y_2=\dfrac {11}{5}+\dfrac{\sqrt{53}}{5}.\end{cases}$
所以 $P_1(3+\sqrt{53},\dfrac {11}{5}-\dfrac{\sqrt{53}}{5})$，$P_2(3-\sqrt{53},\dfrac {11}{5}+\dfrac{\sqrt{53}}{5}))$
【解析】
略
答案
解析
备注
