题目 设函数 $f\left(x\right)=x^2+ax+b\left(a,b\in{\mathbb R}\right)$． 问题1 当 $b=\dfrac{a^2}{4}+1$ 时，求函数 $f\left(x\right)$ 在 $\left[-1,1\right]$ 上的最小值 $g\left(a\right)$ 的表达式； 答案1 $g(a)=\begin{cases} \dfrac 14a^2+a+2,&a\in (-\infty ,-2],\\1,&a\in (-2,2),\\\dfrac 14a^2-a+2,&a\in [2,+\infty ).\end{cases}$ 解析1 当 $b=\dfrac {a^2}4+1$ 时，$f(x)=\left(x+\dfrac a2\right)^2+1$，按 $-\dfrac a2$ 与 $-1,1$ 的大小关系讨论．<br/>当 $a\leqslant -2$ 时，函数 $f(x)$ 在区间 $[-1,1]$ 上单调递减，$g(a)=f(1)=\dfrac 14a^2+a+2$；<br/>当 $-2<a<2$ 时，函数 $f(x)$ 在区间 $\left[-1,-\dfrac a2\right]$ 上单调递减，在区间 $\left[-\dfrac a2,1\right]$ 上单调递增，$g(a)=f\left(-\dfrac a2\right)=1$；<br/>当 $a\geqslant 2$ 时，函数 $f(x)$ 在区间 $[-1,1]$ 上单调递增，$g(a)=f(-1)=\dfrac 14a^2-a+2$．<br/>综上，$g(a)=\begin{cases} \dfrac 14a^2+a+2,&a\in (-\infty ,-2],\\1,&a\in (-2,2),\\\dfrac 14a^2-a+2,&a\in [2,+\infty ).\end{cases}$ 备注1 问题2 已知函数 $f\left(x\right)$ 在 $\left[-1,1\right]$ 上存在零点，$0\leqslant b-2a\leqslant 1$，求 $b$ 的取值范围． 答案2 $\left[-3,9-4\sqrt 5\right]$ 解析2 设函数 $f(x)$ 在区间 $[-1,1]$ 上的零点为 $x=\alpha$．<br/><case>情形一</case> $\alpha=0$ 时，此时 $b=0$．<br/><case>情形二</case> $\alpha\neq 0$ 时，此时 $f(x)$ 有另外一个零点 $x=\dfrac{b}{\alpha}$，于是$$-a=\alpha+\dfrac{b}{\alpha},$$又根据题意 $0\leqslant b-2a\leqslant 1$，即 $-\dfrac b2\leqslant -a\leqslant \dfrac{1-b}2$，因此$$-\dfrac b2\leqslant \alpha+\dfrac{b}{\alpha}\leqslant \dfrac {1-b}2,$$从而 $b$ 在 $\dfrac{\alpha-2\alpha^2}{2+\alpha}$ 与 $\dfrac{-2\alpha^2}{2+\alpha}$ 之间．<br/>令 $t=2+\alpha$，则 $t\in [1,3]$ 且 $t\neq 2$，此时可得 $b$ 在 $9-2\left(t+\dfrac 5t\right)$ 和 $8-2\left(t+\dfrac 4t\right)$ 之间．<br/>在同一个坐标系中画出函数 $b=9-2\left(t+\dfrac 5t\right)$ 与函数 $b=8-2\left(t+\dfrac 4t\right)$ 的图象，如图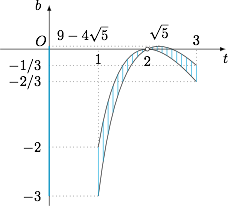．<img src="/static/images/531d31069abc31df0e507a4af12d89e9.png" class="img-responsive" />可得 $b$ 的取值范围为 $\left[-3,0\right)\cup\left(0,9-4\sqrt 5\right]$．<br/>综合以上两种情况可得 $b$ 的取值范围是 $\left[-3,9-4\sqrt 5\right]$． 备注2