已知 $\angle EDF$ 的顶点 $D$ 在 $\triangle ABC$ 的边 $AB$ 所在直线上（不与 $A,B$ 重合）．$DE$ 交 $AC$ 所在直线于点 $M$，$DF$ 交 $BC$ 所在直线于点 $N$．记 $\triangle ADM$ 的面积为 $S_1$，$\triangle BND$ 的面积为 $S_2$．
【难度】
【出处】
无
【标注】
-
如图1，当 $\triangle ABC$ 是等边三角形，$\angle EDF=\angle A$ 时，若 $AB=6,AD=4$，求 $S_1\cdot S_2$ 的值；标注答案$S_1\cdot S_2=12$解析如图，过点 $M,N$ 作 $AB$ 的垂线，垂直分别为点 $G,H$．
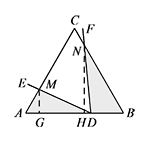$\begin{split}则S_1\cdot S_2&=\dfrac 12MG\cdot AD\cdot \dfrac 12 NH\cdot BD\\ &=\dfrac 14AD\cdot AM\cdot \sin\angle A\cdot BD\cdot BN\cdot\sin\angle B.\end{split}$
由题意可得 $\angle A=\angle B=60^\circ$，
所以 $\sin \angle A=\sin \angle B=\dfrac{\sqrt 3}2$．
由“一线三等角模型”可得 $\triangle AMD\backsim \triangle BDN$，
所以 $\dfrac{AM}{BD}=\dfrac{AD}{BN}$，
从而 $AM\cdot BN=AD\cdot BD=8$，
所以 $S_1\cdot S_2=12$． -
当 $\triangle ABC$ 是等腰三角形时，设 $\angle B=\angle A=\angle EDF=\alpha$．
$(1)$ 如图2，当点 $D$ 在线段 $AB$ 上运动时，设 $AD=a,BD=b$，求 $S_1\cdot S_2$ 的表达式（结果用 $a,b$ 和 $\alpha$ 的三角函数表示）．
$(2)$ 如图3，当点 $D$ 在 $BA$ 的延长线上运动时，设 $AD=a,BD=b$，直接写出 $S_1\cdot S_2$ 的表达式．标注答案$(1)$ $S_1\cdot S_2=\dfrac 14a^2b^2\sin^2\alpha$；
$(2)$ $S_1\cdot S_2=\dfrac 14a^2b^2\sin^2\alpha$解析$(1)$ 如图，过点 $M,N$ 作 $AB$ 的垂线，垂直分别为点 $G,H$．
$\begin{split}则S_1\cdot S_2&=\dfrac 12MG\cdot AD\cdot \dfrac 12 NH\cdot BD\\ &=\dfrac 14AD\cdot AM\cdot \sin\angle A\cdot BD\cdot BN\cdot\sin\angle B.\end{split}$
由“一线三等角模型”可得 $\triangle AMD\backsim \triangle BDN$，
所以 $\dfrac{AM}{BD}=\dfrac{AD}{BN}$，从而 $AM\cdot BN=AD\cdot BD=ab$．
所以 $S_1\cdot S_2=\dfrac 14a^2b^2\sin^2\alpha$；
$(2)$ 如图，过点 $M,N$ 作 $AB$ 的垂线，垂直分别为点 $G,H$．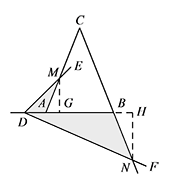
$\begin{split}则S_1\cdot S_2&=\dfrac 12MG\cdot AD\cdot \dfrac 12 NH\cdot BD\\ &=\dfrac 14AD\cdot AM\cdot \sin\angle A\cdot BD\cdot BN\cdot\sin\angle B.\end{split}$
由“一线三等角模型”可得 $\triangle AMD\backsim \triangle BDN$，
所以 $\dfrac{AM}{BD}=\dfrac{AD}{BN}$，从而 $AM\cdot BN=AD\cdot BD=ab$．
所以 $S_1\cdot S_2=\dfrac 14a^2b^2\sin^2\alpha$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
