如图，已知 $\angle ABC=90^\circ $，$D$ 是直线 $AB$ 上的点，$AD=BC$．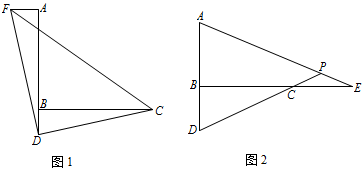
【难度】
【出处】
无
【标注】
-
如图 1，过点 $A$ 作 $AF\perp AB$，并截取 $AF=BD$，连接 $DC$，$DF$，$CF$，判断 $\triangle CDF$ 的形状并证明；标注答案$ \triangle CDF$ 是等腰直角三角形解析
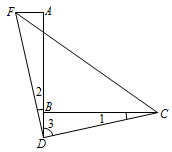因为 $ \angle ABC=90^\circ$，$AF\perp AB$，
所以 $ \angle FAD=\angle DBC$．
因为 $AD=BC$，$AF=BD$，
所以 $ \triangle FAD\cong \triangle DBC$，
所以 $ FD=DC$，$\angle 1 =\angle 2$．
因为 $\angle 1+\angle 3=90^\circ$，
所以 $ \angle 2+\angle 3=90^\circ$，即 $\angle CDF=90^\circ$，
所以 $ \triangle CDF$ 是等腰直角三角形． -
如图2，$E$ 是直线 $BC$ 上的一点，且 $CE=BD$，直线 $AE$，$CD$ 相交于点 $P$，$\angle APD$ 的度数是一个固定的值吗？若是，请求出它的度数，若不是，请说明理由．标注答案固定，$\angle APD=45^\circ$解析如图，过点 $A$ 作 $AF\perp AB$，并截取 $AF=BD$，连接 $DF$，$CF$．
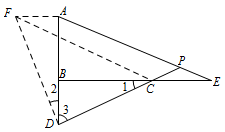因为 $ \angle ABC=90^\circ$，$AF\perp AB$，
所以 $ AF \parallel CE$．
又 $BD=CE$，$AF=BD$，
所以 $ AF=CE$，
所以四边形 $AFCE$ 是平行四边形．
所以 $ FC \parallel AE$，
所以 $ \angle APD=\angle FCD$．
由 $(1)$ 知 $\triangle DAF\cong \triangle CBD$
所以 $\angle 1=\angle 2$，$FD=DC$，
所以 $ \angle FCD=45^\circ$，
所以 $\angle APD=45^\circ$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
