如图，直线 $l:y=-\dfrac 43x+4$ 分别与 $y$ 轴、$x$ 轴交于点 $A,B$，设点 $M$ 在射线 $AB$ 上，将点 $M$ 绕点 $A$ 逆时针旋转 $90^\circ$ 到点 $N$，以点 $N$ 为圆心、$NA$ 的长为半径作 $\odot N$．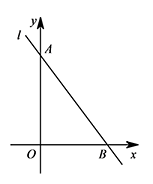
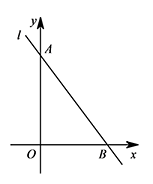
【难度】
【出处】
无
【标注】
-
当 $\odot N$ 与 $x$ 轴相切时，求点 $M$ 的坐标；标注答案点 $M$ 的坐标为 $(6,-4)$解析由直线 $l$ 的解析式可得点 $A(0,4)$，点 $B(3,0)$，
所以 $OA=4$，$OB=3$，$AB=5$．
设点 $M$ 的坐标为 $\left(m,-\dfrac 43m+4\right)$．
如图，分别过点 $M,N$ 作 $y$ 轴的垂线，垂足为点 $F,G$．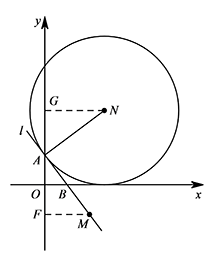
由题意可得点 $N$ 在第一象限，显然 $\triangle MFA\cong \triangle AGN$，
所以 $NG=AF=4-\left(-\dfrac 43m+4\right)=\dfrac 43m$，$AG=MF=m$．
而 $\dfrac{BO}{MF}=\dfrac{AB}{AM}$，所以 $AN=AM=\dfrac 53m$．
如果 $\odot N$ 与 $x$ 轴相切，则由 $OG=AN$，
所以 $m+4=\dfrac 53m$，解得 $m=6$，
所以此时点 $M$ 的坐标为 $(6,-4)$． -
在第1问的条件下，设直线 $AN$ 与 $x$ 轴交于点 $C$，与 $\odot N$ 的另一个交点为点 $D$，连接 $MD$ 交 $x$ 轴于点 $E$，直线 $m$ 过点 $N$ 分别与 $y$ 轴、直线 $l$ 交于点 $P,Q$，当 $\triangle APQ$ 与 $\triangle CDE$ 相似时，求点 $P$ 的坐标．标注答案点 $P$ 的坐标为 $(0,-6)$ 或 $(0,14)$解析由 $(1)$ 可得点 $N$ 的坐标为 $(8,10)$，
所以直线 $AN$ 的解析式为 $y=\dfrac 34x+4$．
所以点 $C$ 的坐标为 $\left(-\dfrac{16}3,0\right)$，
从而 $\tan \angle ACO=\dfrac 34=\tan \angle BAO$，
所以 $\angle ACO=\angle BAO$，可得 $AB\perp CD$．
由点 $N$ 为 $AD$ 的中点，从而得到点 $D$ 的坐标为 $(16,16)$．
所以直线 $DM$ 的解析式为 $y=2x-16$，
所以点 $E$ 的坐标为 $(8,0)$．
连接 $NE$，则 $NE\perp x$ 轴．
所以 $AB,BC$ 均为 $\odot N$ 的切线，切点分别为 $A,E$．
连接 $AE$，则 $\angle D=\angle BAE=\angle BEA$．
设点 $P$ 的坐标为 $(0,n)$．
① 如图，当点 $P,Q$ 在直线 $AN$ 下方时，则 $\angle AQP$ 为钝角．
若 $\triangle APQ$ 与 $\triangle CDE$ 相似，而 $\angle PAQ=\angle DCE$，
所以只能 $\angle APQ=\angle CDE=\angle AEO$．
从而 $\tan \angle APQ=\tan \angle AEO$，即 $\dfrac{NG}{PG}=\dfrac{AO}{EO}$，
所以 $\dfrac{8}{10-n}=\dfrac{4}{8}$，解得 $n=-6$．
所以此时点 $P$ 的坐标为 $(0,-6)$；
② 如图，点点 $P,Q$ 在直线 $AN$ 的上方时，则 $\angle APQ$ 为钝角．
若 $\triangle APQ$ 与 $\triangle CDE$ 相似，则 $\angle APQ=\angle CED$，
所以 $\angle NPA=\angle \alpha=\angle EAO$，
从而 $\tan \angle NPG=\tan \angle EAO$，即 $\dfrac{NG}{PG}=\dfrac{EO}{AO}$，
所以 $\dfrac{8}{n-10}=\dfrac{8}{4}$，解得 $n=14$．
所以此时点 $P$ 的坐标为 $(0,14)$．
综上可得，点 $P$ 的坐标为 $(0,-6)$ 或 $(0,14)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
