如图所示,过双曲线 $x^2-\dfrac{y^2}{4}=1$ 的中心 $O$ 作两条互相垂直的射线,交双曲线于 $A,B$ 两点,试求: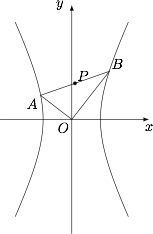

【难度】
【出处】
2011年全国高中数学联赛贵州省预赛
【标注】
-
弦 $AB$ 的中点 $P$ 的轨迹方程;标注答案$3(4x^2-y^2)^2=4(16x^2+y^2)$解析设 $P(x,y)$,$A(x-m,y-n)$,$B(x+m,y+n)$.
由 $A,B$ 在双曲线上得\[\begin{split}&4(x-m)^2-(y-n)^2=4,\\ &4(x+m)^2-(y+n)^2=4,\end{split}\]又 $OA\perp OB$,所以$$\overrightarrow{OA}\cdot \overrightarrow{OB}=0,$$即$$(x-m)(x+m)+(y-n)(y+n)=0,$$即$$x^2+y^2=m^2+n^2.$$利用开始两式消去 $m,n$ 得$$3(4x^2-y^2)^2=4(16x^2+y^2),$$此即为 $P$ 点的轨迹方程. -
双曲线的中心 $O$ 到直线 $AB$ 的距离.标注答案$\dfrac{2\sqrt 3}{3}$解析作 $OC\perp AB$ 于 $C$,则$$OC\cdot AB=OA\cdot OB,$$因为$$x^2+y^2=m^2+n^2,$$所以$$AB^2=4(m^2+n^2)=4(x^2+y^2).$$所以\[\begin{split}OA^2\cdot OB^2&=[(x-m)^2+(y-n)^2][(x+m)^2+(y+n)^2]\\&=(x^2+y^2+m^2+n^2)^2-(2xm+2yn)^2\\&=[2(x^2+y^2)^2]-4(mx+ny)^2.\end{split}\]由 $(1)$ 可得 $4mx=ny$,$m^2=\dfrac{(x^2+y^2)y^2}{16x^2+y^2}$,所以\[\begin{split}OA^2\cdot OB^2&=4(x^2+y^2)^2-100x^2\cdot \dfrac{(x^2+y^2)y^2}{16x^2+y^2}\\&=\dfrac{4(x^2+y^2)(4x^2-y^2)^2}{16x^2+y^2},\end{split}\]故$$OC^2=\dfrac{OA^2\cdot OB^2}{AB^2}=\dfrac{(4x^2-y^2)^2}{16x^2+y^2}.$$又因为$$3(4x^2-y^2)^2=4(16x^2+y^2),$$所以$$OC^2=\dfrac 43,$$即 $OC=\dfrac{2\sqrt 3}{3}$.
因此 $O$ 到 $AB$ 的距离为 $\dfrac{2\sqrt 3}{3}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2