设点 $P$ 为圆 $C_{1}:x^{2}+y^{2}=2$ 上的动点,过点 $P$ 作 $x$ 轴的垂线,垂足为 $Q$.点 $M$ 满足 $\sqrt 2\overrightarrow{MQ}=\overrightarrow{PQ}$.
【难度】
【出处】
2013年全国高中数学联赛辽宁省预赛
【标注】
-
求点 $M$ 的轨迹 $C_{2}$ 的方程;标注答案$\dfrac{x^{2}}{2}+y^{2}=1$解析设点 $M(x,y)$.
因为 $\sqrt 2\cdot \overrightarrow{MQ}=\overrightarrow{PQ}$,所以$$P(x,\sqrt 2y),$$由于点 $P$ 在 $C_{1}:x^{2}+y^{2}=2$ 上,所以$$x^{2}+2y^{2}=2,$$即点 $M$ 的轨迹方程为 $\dfrac{x^{2}}{2}+y^{2}=1$.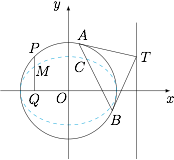
-
过直线 $x=2$ 上的点 $T$ 作圆 $C_{1}$ 的两条切线,设切点分别为 $A,B$,若直线 $AB$ 与第 $(1)$ 小问中的曲线 $C_{2}$ 交于 $C,D$ 两点,求 $\dfrac{|CD|}{|AB|}$ 的取值范围.标注答案$\left[\dfrac{\sqrt 2}{2},1\right)$解析设点 $T(2,t)$,$A(x_{1}',y_{1}')$,$B(x_{2}',y_{2}')$,则 $AT,BT$ 的方程分别为\[x_{1}'x+y_{1}'y=2,x_{2}'x+y_{2}'y=2,\]又点 $T(2,t)$ 在 $AT,BT$ 上,则有:\[\begin{split}2x_{1}'+ty_{1}'&=2,\cdots\cdots\text{ ① }\\ 2x_{2}'+ty_{2}'&=2.\cdots\cdots\text{ ② }\end{split}\]由 ①,② 知 $AB$ 的方程为:$2x+ty=2$.
设点 $C(x_{1},y_{1})$,$D(x_{2},y_{2})$,则圆心 $O$ 到 $AB$ 的距离 $d=\dfrac{2}{\sqrt{4+t^{2}}}$,则\[|AB|=2\sqrt{r^{2}-d^{2}}=2\sqrt{\dfrac{2t^{2}+4}{t^{2}+4}}.\]又由$$\begin{cases}2x+ty=2,\\ \dfrac{x^{2}}{2}+y^{2}=1,\end{cases}$$得$$(t^{2}+8)y^{2}-4ty-4=0,$$于是$$y_{1}+y_{2}=\dfrac{4t}{t^{2}+8},y_{1}y_{2}=\dfrac{-4}{t^{2}+8},$$所以\[|CD|=\sqrt{1+\dfrac{t^{2}}{4}}|y_{1}-y_{2}|=\dfrac{2\sqrt{t^{2}+4}\cdot \sqrt{2t^{2}+8}}{t^{2}+8},\]于是\[\dfrac{|AB|}{|CD|}=\dfrac{(t^{2}+8)\sqrt{t^{2}+2}}{(t^{2}+4)\sqrt{t^{2}+4}}.\]设 $t^{2}+4=s$,则 $s\geqslant 4$,于是\[\dfrac{|AB|}{|CD|}=\sqrt{\dfrac{s^{3}+6s^{2}-32}{s^{3}}}=\sqrt{1+\dfrac{6}{s}-\dfrac{32}{s^{3}}}.\]设 $\dfrac{1}{s}=m$,$m\in\left(0,\dfrac{1}{4}\right]$,于是\[\dfrac{|AB|}{|CD|}=\sqrt{1+6m-32m^{2}}.\]设 $f(m)=1+6m-32m^{3}$,则$$f'(m)=6-96m^{2},$$令 $f'(m)=0$,得 $m=\dfrac{1}{4}$,所以 $f(m)$ 在 $\left(0,\dfrac{1}{4}\right]$ 上单调递增.
因此 $f(m)\in(1,\sqrt 2]$,即 $\dfrac{|CD|}{|AB|}$ 的范围为 $\left[\dfrac{\sqrt 2}{2},1\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2