如图1,直角梯形 $ABCD$,$AB=AD=\dfrac{1}{2}DC=1$.如图2,将 $\triangle ABD$ 沿 $BD$ 折起来,使平面 $ABD\perp \text{平面}BCD$.设 $G$ 为 $AD$ 的中点,$AH=2HC$,$BD$ 的中点为 $O$.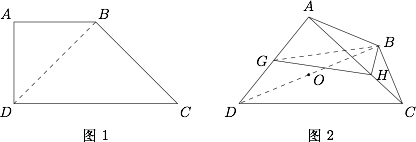

【难度】
【出处】
2016年全国高中数学联赛广东省预赛
【标注】
-
求证:$AO\perp \text{平面}BCD$;标注答案略解析因为 $AB = AD$,$O$ 为 $BD$ 的中点,所以 $AO \perp BD$.
又因为$$\text {平面} ABD \perp\text{ 平面 }BCD,\text { 平面} ABD \cap\text{ 平面 }BCD = BD,$$所以 $AO \perp$ 平面 $BCD$. -
求平面 $GHB$ 与平面 $BCD$ 所成锐二面角的余弦值;标注答案$\dfrac {6\sqrt{41}}{41}$解析取 $DC$ 的中点 $M$,连结 $OM$,则 $OM \parallel BC$.
由图1可知,$$BD = BC = \sqrt 2, DC = 2,$$所以 $BC \perp BD$,从而 $OM \perp BD$.
由第 $(1)$ 小题知,$AO \perp$ 平面 $BCD$,因此 $OA$,$OM$,$BD$ 两两垂直,分别以射线 $OD$,$OM$,$OA$ 为 $x$ 轴,$y$ 轴,$z$ 轴的正方向,建立空间直角坐标系.
读取各点的坐标$$O(0, 0, 0), G\left(\dfrac{\sqrt 2}{4}, 0,\dfrac{\sqrt 2}{4}\right), A\left(0, 0,\dfrac{\sqrt 2}{2}\right), B\left(-\dfrac{\sqrt 2}{2}, 0, 0,\right), C\left(-\dfrac{\sqrt 2}{2}, \sqrt 2, 0,\right).$$因为 $AH=2HC$,所以 $H\left(-\dfrac{\sqrt 2}{3}, \dfrac{2\sqrt 2}{3}, \dfrac{\sqrt 2}{6},\right)$.
设平面 $GHB$ 的法向量为 $\overrightarrow n = (x, y, z)$,则$$\begin{cases}\overrightarrow{GB}\cdot \overrightarrow n = 0, \\ \overrightarrow{GH}\cdot \overrightarrow n = 0,\end{cases}$$故有\[\begin{cases}3x + z = 0, \\ -7x + 8y - z = 0.\end{cases}\]取 $x=1$,则 $\overrightarrow n = \left(1, \dfrac 1 2, -3\right)$.
由 $(1)$ 知,$\overrightarrow{OA}=\left(0, 0,\dfrac{\sqrt 2}{2}\right)$ 是平面 $BCD$ 的法向量,所以平面 $GHB$ 与平面 $BCD$ 所成锐二面角的余弦值为\[\cos \theta = \left| \cos \left\langle\overrightarrow n,\overrightarrow{OA}\right\rangle\right| = \dfrac {6\sqrt{41}}{41}.\] -
在线段 $BC$ 上是否存在点 $E$,使得 $DE\parallel \text{平面}GBH$,若存在确定点 $E$ 的位置,若不存在,说明理由.标注答案不存在,理由略解析假设在线段 $BC$ 上存在点 $E$,使得 $DE \parallel$ 平面 $GBH$,设\[\overrightarrow{BE} = \lambda \overrightarrow{BC}(0<\lambda \leqslant 1),\]所以 $E\left(-\dfrac{\sqrt 2}{2}, \sqrt 2 \lambda, 0\right)$.
又 $D\left(\dfrac{\sqrt 2}{2}, 0, 0\right)$,所以\[\begin{split}\overrightarrow{DE}\cdot \overrightarrow n &=\left(-\sqrt 2, \sqrt 2 \lambda, 0,\right)\cdot \left(1, \dfrac 1 2, -3\right)\\ &=\dfrac{\sqrt 2}{2} \lambda - \sqrt 2 =0,\end{split}\]因此 $\lambda = 2$,这与 $0<\lambda \leqslant 1$ 矛盾.
因此在线段 $BC$ 上不存在点 $E$,使得 $DE \parallel$ 平面 $GBH$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3