如图,点 $P$ 在 $\triangle ABC$ 的边 $AB$ 上,且 $AB=4AP$,过点 $P$ 的直线 $MN$ 与 $\triangle ABC$ 的外接圆交于点 $M,N$,且点 $A$ 是弧 $MN$ 的中点.求证: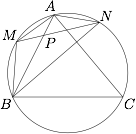

【难度】
【出处】
2016年全国高中数学联赛江苏省预赛(初赛)
【标注】
-
$\triangle ABN\backsim \triangle ANP$;标注答案略解析因为点 $A$ 是弧 $MN$ 的中点,所以$$\angle ANM=\angle AMN=\angle ABN.$$又因为$$\angle BAN=\angle NAP,$$所以 $\triangle ABN\sim \triangle ANP$.
-
$BM+BN=2MN$.标注答案略解析由第 $(1)$ 小问知,$$\dfrac{AB}{AN}=\dfrac{AN}{AP}=\dfrac{BN}{NP}.$$又 $AB=4AP$,所以 $AN=2AP$,从而 $\dfrac{BN}{NP}=2$,即$$BN=2NP.$$同理 $BM=2MP$,所以$$BM+BN=2MN.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2