如图,椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F$,过点 $F$ 的直线交椭圆于 $A,B$ 两点,$|AF|$ 的最大值是 $M$,$|BF|$ 的最小值是 $m$,满足 $M\cdot m=\dfrac34a^2$.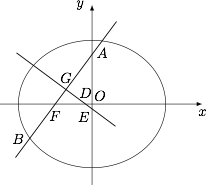

【难度】
【出处】
2015年全国高中数学联赛黑龙江省预赛
【标注】
-
求该椭圆的离心率;标注答案$\dfrac12$解析设椭圆的半焦距为 $c$,则根据椭圆的性质得$$M=a+c,m=a-c,$$根据题意有$$M\cdot m=(a+c)(a-c)=\dfrac34a^2,$$整理得 $a=2c$,因此椭圆的离心率为 $\dfrac{c}{a}=\dfrac12$.
-
设线段 $AB$ 的中点为 $G$,$AB$ 的垂直平分线与 $x$ 轴和 $y$ 轴分别交于 $D,E$ 两点,$O$ 是坐标原点.记 $\triangle GFD$ 的面积为 $S_1$,$\triangle OED$ 的面积为 $S_2$,求 $\dfrac{2S_1S_2}{S_1^2+S_2^2}$ 的取值范围.标注答案$\left(0,\dfrac{9}{41}\right)$解析由 $(1)$ 可知$$a=2c,b=\sqrt3c,$$则椭圆方程可表示为$$\dfrac{x^2}{4c^2}+\dfrac{y^2}{3c^2}=1.$$设 $A(x_1,y_1),B(x_2,y_2)$.
根据条件直线 $AB$ 的斜率一定存在且不为零,设直线 $AB$ 的方程为$$y=k(x+c),$$与椭圆方程联立,消去 $y$ 得$$(4k^2+3)x^2+8ck^2x+4k^2c^2-12c^2=0,$$从而\[\begin{split}&x_1+x_2=-\dfrac{8ck^2}{4k^2+3},\\&y_1+y_2=k(x_1+x_2+2c)=\dfrac{6ck}{4k^2+3},\end{split}\]所以 $G\left(-\dfrac{4ck^2}{4k^2+3},\dfrac{3ck}{4k^2+3}\right)$.
因为 $DG\perp AB$,所以$$\dfrac{\frac{3ck}{4k^2+3}}{-\frac{4ck^2}{4k^2+3}-x_D}\cdot k=-1,$$即$$x_D=-\dfrac{ck^2}{4k^2+3}.$$由于 $\triangle FGD\backsim\triangle EOD$,所以$$\dfrac{S_1}{S_2}=\dfrac{GD^2}{OD^2}=\dfrac{\left(-\frac{4ck^2}{4k^2+3}+\frac{ck^2}{4k^2+3}\right)^2+\left(\frac{3ck}{4k^2+3}\right)^2}{\left(-\frac{ck^2}{4k^2+3}\right)^2}=9+\dfrac{9}{k^2}>9.$$令 $\dfrac{S_1}{S_2}=t$,则 $t>9$,从而$$\dfrac{2S_1S_2}{S_1^2+S_2^2}=\dfrac{2}{t+\frac1t}<\dfrac{2}{9+\frac19}=\dfrac{9}{41},$$故 $\dfrac{2S_1S_2}{S_1^2S_2^2}$ 的取值范围是 $\left(0,\dfrac{9}{41}\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2