如图,已知两点 $A(-\sqrt 5,0),B(\sqrt 5,0)$,$\triangle{ABC}$ 的内切圆的圆心在直线 $x=2$ 上移动.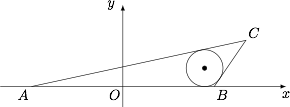

【难度】
【出处】
2009年全国高中数学联赛陕西省预赛(一试)
【标注】
-
求点 $C$ 的轨迹方程;标注答案$\dfrac{x^2}{4}-y^2=1(x>2)$解析设 $\triangle{ABC}$ 内切圆切 $AB$ 边于点 $D$,则\[\begin{split}&|CA|-CB|\\=&|AD|-|BD|\\=&(\sqrt 5+2)-(\sqrt 5 -2)\\=&4<2\sqrt 5,\end{split}\]所以,点 $C$ 的轨迹是以 $A,B$ 为焦点,实轴长为 $4$ 的双曲线的右支(不含右顶点),其方程为$$\dfrac{x^2}{4}-y^2=1(x>2).$$
-
过点 $M(2,0)$ 作两条射线,分别交 $(1)$ 中所求轨迹于 $P,Q$ 两点,且 $\overrightarrow{MP}\cdot \overrightarrow{MQ}=0$.求证:直线 $PQ$ 必过定点.标注答案略解析设 $PQ:x=my+a$($a>2$),代入 $\dfrac{x^2}{4}-y^2=1$,得$$(m^2-4)y^2+2amy+a^2-4=0.$$设 $P(x_1,y_1)$,$Q(x_2,y_2)$,则$$\begin{cases}y_1+y_2=-\dfrac{2am}{m^2-4},\\ y_1y_2=\dfrac{a^2-4}{m^2-4}.\end{cases}$$因为\[\begin{split}\overrightarrow{MP}\cdot \overrightarrow{MQ}&=(x_1-2)(x_2-2)+y_1y_2\\&=(my_1+a-2)(my_2+a-2)+y_1y_2\\&=(m^2+1)y_1y_2+m(a-2)(y_1+y_2)+(a-2)^2\\&=0,\end{split}\]所以$$\dfrac{(m^2+1)(a^2-4)}{m^2-4}-\dfrac{2am^2(a-2)}{m^2-4}+(a-2)^2=0,$$化简得$$3a^2-16a+20=0,$$解得 $a=2$(舍)或 $a=\dfrac{10}{3}$,故直线 $PQ$ 必过定点 $\left(\dfrac{10}{3},0\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2