已知 $\triangle ABC$ 中，$M$ 为 $BC$ 的中点，直线 $m$ 绕点 $A$ 旋转，过 $B,M,C$ 分别作 $BD\perp m$ 于点 $D$，$ME\perp m$ 于点 $E$，$CF\perp m$ 于点 $F$．
当直线 $m$ 经过 $B$ 点时，如图 1，易证 $EM={\dfrac{1}{2}}CF$，当直线 $m$ 不经过 $B$ 点，旋转到如图 2 、图 3 的位置时，线段 $BD,ME,CF$ 之间有怎样的数量关系？请直接写出你的猜想，并选择一种情况加以证明．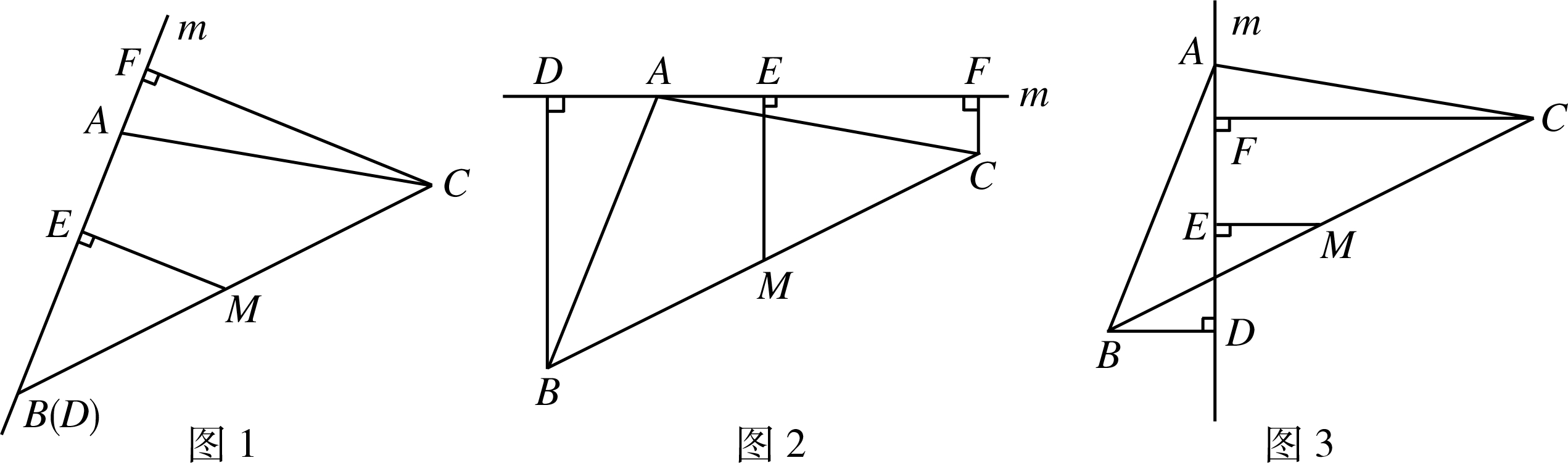
当直线 $m$ 经过 $B$ 点时，如图 1，易证 $EM={\dfrac{1}{2}}CF$，当直线 $m$ 不经过 $B$ 点，旋转到如图 2 、图 3 的位置时，线段 $BD,ME,CF$ 之间有怎样的数量关系？请直接写出你的猜想，并选择一种情况加以证明．
【难度】
【出处】
无
【标注】
【答案】
图 2 的结论为 $ME={\dfrac{1}{2}}\left(BD+CF\right)$．
图 3 的结论为 $ME={\dfrac{1}{2}}\left(CF-BD\right)$．
图 2 的结论证明如下：
连接 $DM$ 并延长交 $FC$ 的延长线于点 $K$，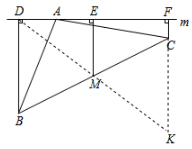
因为 $ BD\perp m$，$CF\perp m$，
所以 $BD\parallel CF$，
所以 $\angle DBM=\angle KCM$．
因为 $ \angle DMB=\angle CMK$，$BM=MC$，
所以 $ \triangle DBM \cong \triangle KCM$，
所以 $ DB=CK$，$DM=MK$．
由 $(1)$ 知 $EM={\dfrac{1}{2}}FK$，
所以 $ME={\dfrac{1}{2}}\left(CF+CK\right)={\dfrac{1}{2}}\left(CF+DB\right)$．
图 3 的结论证明如下：
连接 $DM$ 并延长交 $FC$ 于点 $K$，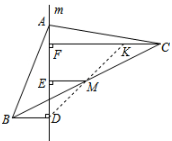
因为 $BD\perp m$，$CF\perp m$，
所以 $ BD\parallel CF$，
所以 $ \angle MBD=\angle KCM$．
因为 $\angle DMB=\angle CMK$，$BM=MC$，
所以 $ \triangle DBM \cong \triangle KCM$，
所以 $DB=CK $，$DM=MK$，
由 $(1)$ 知 $EM={\dfrac{1}{2}}FK$，
所以 $ME={\dfrac{1}{2}}\left(CF-CK\right)={\dfrac{1}{2}}\left(CF-DB\right)$．
图 3 的结论为 $ME={\dfrac{1}{2}}\left(CF-BD\right)$．
图 2 的结论证明如下：
连接 $DM$ 并延长交 $FC$ 的延长线于点 $K$，
因为 $ BD\perp m$，$CF\perp m$，所以 $BD\parallel CF$，
所以 $\angle DBM=\angle KCM$．
因为 $ \angle DMB=\angle CMK$，$BM=MC$，
所以 $ \triangle DBM \cong \triangle KCM$，
所以 $ DB=CK$，$DM=MK$．
由 $(1)$ 知 $EM={\dfrac{1}{2}}FK$，
所以 $ME={\dfrac{1}{2}}\left(CF+CK\right)={\dfrac{1}{2}}\left(CF+DB\right)$．
图 3 的结论证明如下：
连接 $DM$ 并延长交 $FC$ 于点 $K$，
因为 $BD\perp m$，$CF\perp m$，所以 $ BD\parallel CF$，
所以 $ \angle MBD=\angle KCM$．
因为 $\angle DMB=\angle CMK$，$BM=MC$，
所以 $ \triangle DBM \cong \triangle KCM$，
所以 $DB=CK $，$DM=MK$，
由 $(1)$ 知 $EM={\dfrac{1}{2}}FK$，
所以 $ME={\dfrac{1}{2}}\left(CF-CK\right)={\dfrac{1}{2}}\left(CF-DB\right)$．
【解析】
无
答案
解析
备注
