如图，矩形纸片 $ABCD$ 中，$AB=6$，$BC=8$．折叠纸片使点 $B$ 落在 $AD$ 上，落点为 $B'$．点 $B'$ 从点 $A$ 开始沿 $AD$ 移动，折痕所在直线 $l$ 的位置也随之改变，当直线 $l$ 经过点 $A$ 时，点 $B'$ 停止移动，连接 $BB'$．设直线 $l$ 与 $AB$ 相交于点 $E$，与 $CD$ 所在直线相交于点 $F$，点 $B'$ 的移动距离为 $x$，点 $F$ 与点 $C$ 的距离为 $y$．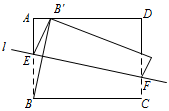
【难度】
【出处】
无
【标注】
-
求证：$\angle BEF=\angle AB'B$；标注答案略解析如图，由四边形 $ABCD$ 是矩形和折叠的性质可知，$BE=B'E$，$\angle BEF=\angle B'EF$，
所以在等腰 $\triangle BEB'$ 中，$EF$ 是角平分线，
所以 $EF\perp BB'$，$\angle BOE=90^\circ $，
所以 $\angle ABB'+\angle BEF=90^\circ $．
因为 $ \angle ABB'+\angle AB'B=90^\circ $，
所以 $\angle BEF=\angle AB'B$． -
求 $y$ 与 $x$ 的函数关系式，并直接写出 $x$ 的取值范围．标注答案$y= \begin{cases}\dfrac{1}{12}x^2-\dfrac43x+3\left(0<x\leqslant 8-2\sqrt7\right)\\-\dfrac1{12}x^2+\dfrac43x-3\left(8-2\sqrt7 <x\leqslant 6\right).\end{cases}$解析① 当点 $F$ 在 $CD$ 之间时，如图，作 $FM\perp AB$ 交 $AB$ 于点 $E$，
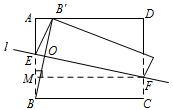因为 $ AB=6$，$BE=EB'$，$AB'=x$，$BM=FC=y$，
所以在 $\mathrm {Rt}\triangle EAB'$ 中，$EB'^2=AE^2+AB'^2$，
所以 $\left(6-AE\right)^2=AE^2+x^2$，解得 $AE=\dfrac{36-x^2}{12}$，
$\tan \angle AB'B= \dfrac{AB}{AB'}=\dfrac6x$，$\tan \angle BEF=\dfrac{MF}{EM} =\dfrac{8}{6-y-\dfrac{36-x^2}{12}}$，
因为由 $(1)$ 知 $\angle BEF=\angle AB'B$，
所以 $\dfrac6x=\dfrac{8}{6-y-\dfrac{36-x^2}{12}}$，
化简，得 $y= \dfrac{1}{12}x^2-\dfrac43x+3$（$0<x\leqslant 8-2\sqrt7$）
② 当点 $F$ 在点 $C$ 下方时，如图所示．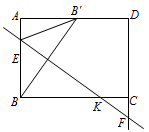
设直线 $EF$ 与 $BC$ 交于点 $K$，
设 $\angle ABB'=\angle BKE=\angle CKF=\theta$，则 $\tan \theta= \dfrac{AB'}{AB}=\dfrac x6$．
$BK=\dfrac{BE}{\tan \theta}$，$CK=BC-BK=8-\dfrac{BE}{\tan \theta}$．
所以 $ CF=CK\cdot \tan \theta=\left(8-\dfrac{BE}{\tan \theta}\right)\cdot \tan \theta=8\tan \theta-BE=\dfrac43x-BE$．
在 $\mathrm {Rt}\triangle EAB'$ 中，$EB'^2=AE^2+AB'^2$，
所以 $\left(6-BE\right)^2+x^2=BE^2$，解得 $BE=\dfrac{36+x^2}{12}$．
所以 $ CF=\dfrac43x-BE=\dfrac43x-\dfrac{36+x^2}{12}=-\dfrac1{12} x^2+\dfrac43x-3$，
所以 $ y=-\dfrac1{12}x^2+\dfrac43x-3$（$8-2\sqrt7 <x\leqslant 6$）．
综上所述，
$y= \begin{cases}\dfrac{1}{12}x^2-\dfrac43x+3\left(0<x\leqslant 8-2\sqrt7\right)\\-\dfrac1{12}x^2+\dfrac43x-3\left(8-2\sqrt7 <x\leqslant 6\right).\end{cases}$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
