如图，$D,E$ 分别为 $\triangle ABC$ 的边 $AB$，$AC$ 上的点，且不与 $\triangle ABC$ 的顶点重合．已知 $AE$ 的长为 $m$，$AC$ 的长为 $n$，$AD$，$AB$ 的长是关于 $x$ 的方程 ${x^2} - 14x + mn = 0$ 的两个根．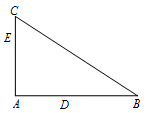
【难度】
【出处】
无
【标注】
-
证明：$C$、$B$、$D$、$E$ 四点共圆；标注答案解析连接 $DE$，
根据题意在 $\triangle ADE$ 和 $\triangle ACB$ 中，\[AD \times AB = mn = AE \times AC,\]即\[\dfrac{{AD}}{{AC}} = \dfrac{{AE}}{{AB}}.\]又 $\angle DAE = \angle CAB$，从而 $\triangle ADE \backsim \triangle ACB$，因此\[\angle ADE = \angle ACB,\]所以 $C$、$B$、$D$、$E$ 四点共圆． -
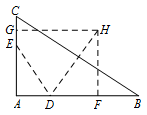
若 $\angle A = 90^\circ $，且 $m = 4$，$n = 6$，求 $C,B,D,E$ 所在圆的半径．标注答案解析$m = 4$，$n = 6$ 时，方程 ${x^2} - 14x + mn = 0$ 的两根为\[{x_1} = 2,{x_2} = 12.\]故\[AD = 2,AB = 12.\]取 $CE$ 的中点 $G$，$DB$ 的中点 $F$，分别过 $G$，$F$ 作 $AC$，$AB$ 的垂线，两垂线相交于 $H$ 点，连接 $DH$．
因为 $C$、$B$、$D$、$E$ 四点共圆，所以 $C$、$B$、$D$、$E$ 四点所在圆的圆心为 $H$，半径为 $DH$．
由于 $\angle A = 90^\circ $，故 $GH\parallel AB$，$HF\parallel AC$．\[\begin{split}HF &= AG = 5 , \\ DF &= \dfrac{1}{2}\left(12 - 2\right) = 5.\end{split}\]故 $C$、$B$、$D$、$E$ 四点所在圆的半径为 $5\sqrt 2 $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
