在如图所示的三棱柱中，点 $A$，$B{B_1}$ 的中点 $M$，以及 ${B_1}{C_1}$ 的中点 $N$ 所决定的平面把三棱柱切割成体积不相同的两部分，问小部分的体积和大部分的体积比为 \((\qquad)\) 
【难度】
【出处】
2008年复旦大学优秀高中生文化水平选拔测试
【标注】
【答案】
D
【解析】
如图，设三棱柱的底面积和高分别为 $S$ 和 $h$，延长 $NM$ 交 $BC$ 于 $Q$，延长 $MN,AF$ 交于 $P$，则\[P\in BCC_1B_1\cap ACC_1A_1=CC_1,\]有\[BQ=B_1N=\dfrac 12BC,\]从而\[\dfrac {C_1F}{C_1A_1}=\dfrac {C_1N}{CQ}=\dfrac 13,\]因此\[{C_1}F = \dfrac{1}{3}{A_1}{C_1}, {C_1}N = \dfrac{1}{2}{B_1}{C_1},\]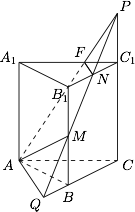
所以$${S_{\triangle {C_1}FN}} = \dfrac{1}{6}S, BQ = \dfrac{1}{2}{B_1}{C_1},$$因此$${S_{\triangle ABQ}} = \dfrac{1}{2}S.$$而$$P{C_1} = MB = \dfrac{1}{2}h,$$所以较大一部分的体积为\begin{align*}
&{V_{P - AQC}} - {V_{P - FN{C_1}}} - {V_{M - ABQ}}\\
={}&\dfrac{1}{3} \cdot \dfrac{3}{2}S \cdot \dfrac{3}{2}h - \dfrac{1}{3} \cdot \dfrac{1}{6}S \cdot \dfrac{1}{2}h - \dfrac{1}{3} \cdot \dfrac{1}{2}S \cdot \dfrac{1}{2} \cdot h\\
={}&\dfrac{{23}}{{36}}Sh.
\end{align*}故所求的体积比为$$\dfrac{{36 - 23}}{{23}} = \dfrac{{13}}{{23}}.$$
所以$${S_{\triangle {C_1}FN}} = \dfrac{1}{6}S, BQ = \dfrac{1}{2}{B_1}{C_1},$$因此$${S_{\triangle ABQ}} = \dfrac{1}{2}S.$$而$$P{C_1} = MB = \dfrac{1}{2}h,$$所以较大一部分的体积为\begin{align*}&{V_{P - AQC}} - {V_{P - FN{C_1}}} - {V_{M - ABQ}}\\
={}&\dfrac{1}{3} \cdot \dfrac{3}{2}S \cdot \dfrac{3}{2}h - \dfrac{1}{3} \cdot \dfrac{1}{6}S \cdot \dfrac{1}{2}h - \dfrac{1}{3} \cdot \dfrac{1}{2}S \cdot \dfrac{1}{2} \cdot h\\
={}&\dfrac{{23}}{{36}}Sh.
\end{align*}故所求的体积比为$$\dfrac{{36 - 23}}{{23}} = \dfrac{{13}}{{23}}.$$
题目
答案
解析
备注
