叙述：
余弦定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦之积的两倍．或：在 $\triangle ABC$ 中，$a$，$b$，$c$ 为 $A$，$B$，$C$ 的对边，有\[\begin{split}{a^2} &= {b^2} + {c^2} - 2bc\cos A , \\
{b^2} &= {c^2} + {a^2} - 2ca\cos B, \\
{c^2} &= {a^2} + {b^2} - 2ab\cos C.\end{split}\]证法一：
如图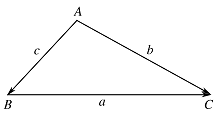，\[\begin{split}{a^2} & = \left|\overrightarrow {BC} \right|^2 = \left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \cdot \left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \\&
= {\overrightarrow {AC} ^2} - 2\overrightarrow {AC} \cdot \overrightarrow {AB} + {\overrightarrow {AB} ^2} \\& = {\overrightarrow {AC} ^2} - 2\left| {\overrightarrow {AC} } \right| \cdot \left| {\overrightarrow {AB} } \right|\cos A +{ {\overrightarrow {AB}}}^2 \\&
= {b^2} - 2bc\cos A + {c^2},\end{split}\]即\[{a^2} = {b^2} + {c^2} - 2bc\cos A.\]同理可证\[\begin{split}{b^2} &= {c^2} + {a^2} - 2ca\cos B,\\ {c^2} &= {a^2} + {b^2} - 2ab\cos C.\end{split}\]证法二：
已知 $\triangle ABC$ 中，$A$，$B$，$C$ 所对边分别为 $a$，$b$，$c$，以 $A$ 为原点，$AB$ 所在直线为 $x$ 轴建立直角坐标系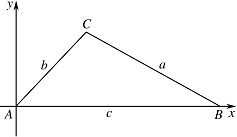，则 $C\left(b\cos A,b\sin A\right)$，$B\left( {c,0} \right)$，所以\[\begin{split}{a^2} & = |BC|^2 = {\left(b\cos A - c\right)^2} + {\left(b\sin A\right)^2} \\&
= {b^2}{\cos ^2}A - 2bc\cos A + {c^2} + {b^2}{\sin ^2}A \\&
= {b^2} + {c^2} - 2bc\cos A,\end{split}\]即\[{a^2} = {b^2} + {c^2} - 2bc\cos A.\]同理可证\[\begin{split}{b^2} &= {c^2} + {a^2} - 2ca\cos B, \\
{c^2} &= {a^2} + {b^2} - 2ab\cos C.\end{split}\]