如图,从点 ${P_1}\left( {0,0} \right)$ 作 $x$ 轴的垂线交曲线 $y = {{\mathrm{e}}^x}$ 于点 ${Q_1}\left( {0,1} \right)$,曲线在 ${Q_1}$ 点处的切线与 $x$ 轴交于点 ${P_2}$,再从 ${P_2}$ 作 $x$ 轴的垂线交曲线于点 ${Q_2}$,依次重复上述过程得到一系列点:${P_1}$,${Q_1}$;${P_2}$,${Q_2}$;$\cdots $;${P_n}$,${Q_n}$,记 $P_k$ 点的坐标为 $\left({x_k},0\right)$ $\left(k = 1,2,\cdots ,n\right)$.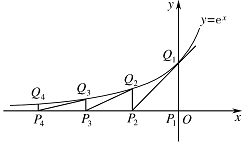

【难度】
【出处】
无
【标注】
-
试求 ${x_k}$ 与 ${x_{k - 1}}$ 的关系 $\left(2 \leqslant k \leqslant n\right)$;标注答案解析设 ${P_{k - 1}}\left({x_{k - 1}},0\right)$,由 $y' = {{\mathrm{e}}^x}$ 得 ${Q_{k - 1}}\left({x_{k - 1}},{{\mathrm{e}}^{{x_{k - 1}}}}\right)$ 点处切线方程为\[y - {{\mathrm{e}}^{{x_{k - 1}}}} = {{\mathrm{e}}^{{x_{k - 1}}}}\left(x - {x_{k - 1}}\right).\]由 $y = 0$ 得\[{x_k} = {x_{k - 1}} - 1 \left(2 \leqslant k \leqslant n\right).\]
-
求 $\left| {{P_1}{Q_1}} \right| + \left| {{P_2}{Q_2}} \right| + \left| {{P_3}{Q_3}} \right| + \cdots + \left| {{P_n}{Q_n}} \right|$.标注答案解析${x_1} = 0$,${x_k} - {x_{k - 1}} = - 1$,得\[{x_k} = - \left(k - 1\right),\]所以 $\left| {{P_k}{Q_k}} \right| = {{\mathrm{e}}^{x_k}} = {{\mathrm{e}}^{ - \left(k - 1\right)}}$,故\[\begin{split} \left| {{P_1}{Q_1}} \right| + \left| {{P_2}{Q_2}} \right| + \left| {{P_3}{Q_3}} \right| + \cdots + \left| {{P_n}{Q_n}} \right| & = 1 + {{\mathrm{e}}^{ - 1}} + {{\mathrm{e}}^{ - 2}} + \cdots + {{\mathrm{e}}^{ - \left(n - 1\right)}} \\&= \dfrac{{1 - {{\mathrm{e}}^{ - n}}}}{{1 - {{\mathrm{e}}^{ - 1}}}} \\&= \dfrac{{{\mathrm{e}} - {{\mathrm{e}}^{1 - n}}}}{{{\mathrm{e}} - 1}}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2