设函数 $f(x)=2x-\cos x$，$\{a_{n}\}$ 是公差为 $\dfrac{\pi}{8}$ 的等差数列，\[f(a_{1})+f(a_{2})+\cdots+f(a_{5})=5\pi,\]则 $[f(a_{3})]^{2}-a_{1}a_{5}=$ \((\qquad)\)
【难度】
【出处】
2012年高考四川卷（理）
【标注】
【答案】
D
【解析】
由于函数 $y=\cos x$ 有无数个对称中心 $\left(k{\mathrm \pi}+\dfrac{\mathrm \pi} 2,0\right)$，其中 $k\in\mathbb Z$，而函数 $y=2x$ 也有无数个对称中心 $\left(x_0,2x_0\right)$，其中 $x_0\in\mathbb R$．因此可得函数 $f(x)=2x-\cos x$ 有无数个对称中心，如图．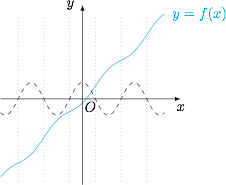
在题目条件的提示下可以选取一个好用的：$$f\left(\dfrac{\mathrm \pi} 2+x\right)+f\left(\dfrac{\mathrm \pi} 2-x\right)=2{\mathrm \pi}.$$结合 $f(x)$ 单调递增，不难得到$$\left\{a_n\right\}:\dfrac{\mathrm \pi} 4,\dfrac{3{\mathrm \pi}}8,\dfrac{\mathrm \pi} 2,\dfrac{5{\mathrm \pi}}8,\dfrac{3{\mathrm \pi}}4.$$进而可得$$\left[f(a_3)\right]^2-a_1a_5={\mathrm \pi}^2-\dfrac{3}{16}{\mathrm \pi}^2=\dfrac{13}{16}{\mathrm \pi}^2.$$
在题目条件的提示下可以选取一个好用的：$$f\left(\dfrac{\mathrm \pi} 2+x\right)+f\left(\dfrac{\mathrm \pi} 2-x\right)=2{\mathrm \pi}.$$结合 $f(x)$ 单调递增，不难得到$$\left\{a_n\right\}:\dfrac{\mathrm \pi} 4,\dfrac{3{\mathrm \pi}}8,\dfrac{\mathrm \pi} 2,\dfrac{5{\mathrm \pi}}8,\dfrac{3{\mathrm \pi}}4.$$进而可得$$\left[f(a_3)\right]^2-a_1a_5={\mathrm \pi}^2-\dfrac{3}{16}{\mathrm \pi}^2=\dfrac{13}{16}{\mathrm \pi}^2.$$
题目
答案
解析
备注
