如图,四棱锥 $ P-ABCD $ 中,底面 $ ABCD $ 为菱形,$ PA\perp $ 底面 $ ABCD$,$AC=2{\sqrt{2}}$,$PA=2 $,$ E $ 是 $ PC $ 上的一点,$ PE=2EC $.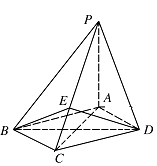

【难度】
【出处】
无
【标注】
-
证明:$ PC\perp $ 平面 $ BED $;标注答案解析方法一:
因为底面 $ ABCD $ 为菱形,所以 $ BD\perp AC $,
又 $ PA\perp $ 底面 $ ABCD $,所以 $ PA\perp BD $,所以 $BD\perp $ 面 $PAC$,所以 $BD\perp PC$.
设 $ AC\cap BD=F $,连接 $ EF $.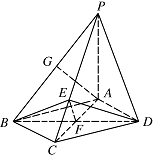 因为 $ AC=2{\sqrt{2}},PA=2,PE=2EC $,故\[PC=2{\sqrt{3}},EC={\dfrac{2{\sqrt{3}}}{3}},FC={\sqrt{2}} ,\]从而\[{\dfrac{PC}{FC}}={\sqrt{6}}, {\dfrac{AC}{EC}}={\sqrt{6}} .\]因为 $ {\dfrac{PC}{FC}}={\dfrac{AC}{EC}},\angle FCE=\angle PCA $,所以\[ \triangle FCE \backsim \triangle PCA,\]从而\[\angle FEC=\angle PAC=90^\circ ,\]由此知 $ PC\perp EF $.
因为 $ AC=2{\sqrt{2}},PA=2,PE=2EC $,故\[PC=2{\sqrt{3}},EC={\dfrac{2{\sqrt{3}}}{3}},FC={\sqrt{2}} ,\]从而\[{\dfrac{PC}{FC}}={\sqrt{6}}, {\dfrac{AC}{EC}}={\sqrt{6}} .\]因为 $ {\dfrac{PC}{FC}}={\dfrac{AC}{EC}},\angle FCE=\angle PCA $,所以\[ \triangle FCE \backsim \triangle PCA,\]从而\[\angle FEC=\angle PAC=90^\circ ,\]由此知 $ PC\perp EF $.
$ PC $ 与平面 $ BED $ 内两条相交直线 $ BD,EF $ 都垂直,
所以 $ PC\perp $ 平面 $ BED $.
方法二:
以 $ A $ 为坐标原点,射线 $ AC $ 为 $ x $ 轴的正半轴,建立如图所示的空间直角坐标系 $ A-xyz $.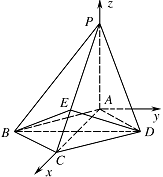 设 $ C\left(2{\sqrt{2}},0,0\right),D\left({\sqrt{2}},b,0\right) $,其中 $ b>0 $,则 $ P\left(0,0,2\right)$,$E \left({\dfrac{4{\sqrt{2}}}{3}},0,{\dfrac{2}{3}}\right)$,$B\left({\sqrt{2}},-b,0\right) $.
设 $ C\left(2{\sqrt{2}},0,0\right),D\left({\sqrt{2}},b,0\right) $,其中 $ b>0 $,则 $ P\left(0,0,2\right)$,$E \left({\dfrac{4{\sqrt{2}}}{3}},0,{\dfrac{2}{3}}\right)$,$B\left({\sqrt{2}},-b,0\right) $.
于是\[ \begin{split}{\overrightarrow {PC}}&=\left(2{\sqrt{2}},0,-2\right),\\ {\overrightarrow {BE}}&= \left({\dfrac{{\sqrt{2}}}{3}},b,{\dfrac{2}{3}}\right) ,\\ {\overrightarrow {DE}}&=\left( {\dfrac{{\sqrt{2}}}{3}},-b,{\dfrac{2}{3}} \right),\end{split}\]从而\[ {\overrightarrow {PC}}\cdot {\overrightarrow {BE}}=0,\\ {\overrightarrow {PC}}\cdot {\overrightarrow {DE}}=0, \]故 $ PC\perp BE,PC\perp DE $.
又 $ BE\cap DE=E $,所以 $ PC\perp $ 平面 $ BDE $. -
设二面角 $ A-PB-C$ 为 $90^\circ $,求 $ PD $ 与平面 $ PBC $ 所成角的大小.标注答案解析$ {\overrightarrow {AP}}=\left(0,0,2\right),{\overrightarrow {AB}}=\left({\sqrt{2}},-b,0\right) $.
设 $\overrightarrow m=\left(x,y,z\right) $ 为平面 $ PAB $ 的法向量,则 $ \overrightarrow m\cdot {\overrightarrow {AP}}=0,\overrightarrow m\cdot {\overrightarrow {AB}}=0 $,
即 $ 2z=0 $ 且 $ {\sqrt{2}}x-by=0$,令 $ x=b $,则 $\overrightarrow m=\left(b, {\sqrt{2}},0\right) $.
设 $\overrightarrow n=\left(p,q,r\right) $ 为平面 $ PBC $ 的法向量,则 $ \overrightarrow n\cdot {\overrightarrow {PC}}=0,\overrightarrow n\cdot {\overrightarrow {BE}}=0$,
即 $ 2{\sqrt{2}}p-2r=0 $ 且 $ {\dfrac{{\sqrt{2}}p}{3}}+bq+{\dfrac{2}{3}}r=0 $.
令 $ p=1 $,则 $ r={\sqrt{2}},q=-{\dfrac{{\sqrt{2}}}{b}},\overrightarrow n= \left(1,-{\dfrac{{\sqrt{2}}}{b}}, {\sqrt{2}} \right)$,
因为平面 $ PAB\perp $ 平面 $ PBC $,故 $ \overrightarrow m\cdot \overrightarrow n=0 $,
即 $ b-{\dfrac{2}{b}}=0 $,故 $ b={\sqrt{2}} $,于是\[\overrightarrow n=\left(1,-1, {\sqrt{2}}\right),{\overrightarrow {DP}}=\left(-{\sqrt{2}},-{\sqrt{2}},2\right) ,\]所以\[ \cos \left \langle\overrightarrow n,{\overrightarrow {DP}}\right \rangle=\dfrac { \overrightarrow n\cdot {\overrightarrow {DP}} }{\left|\overrightarrow n \right| \left|{\overrightarrow {DP}} \right| }={\dfrac{1}{2}} ,\]所以\[ \left \langle \overrightarrow n,{\overrightarrow {DP}}\right \rangle=60^\circ .\]因为 $ PD $ 与平面 $ PBC $ 所成角和 $\left \langle \overrightarrow n,{\overrightarrow {DP}}\right \rangle $ 互余,
故 $ PD $ 与平面 $ PBC $ 所成的角为 $ 30^\circ $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2