如图,在平面直角坐标系 $ xOy $ 中,椭圆 $ {\dfrac{x^2}{a^2}}+{\dfrac{y^2}{b^2}}=1\left(a>b>0\right) $ 的左、右焦点分别为 $ F_1\left(-c,0\right)$,$F_2\left(c,0\right) $,已知点 $ \left(1,{\mathrm {e}}\right) $ 和 $\left( {\mathrm { e}},{\dfrac{{\sqrt{3}}}{2}} \right) $ 都在椭圆上,其中 ${\mathrm { e}} $ 为椭圆的离心率.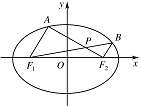

【难度】
【出处】
无
【标注】
-
求椭圆的方程;标注答案椭圆的方程是\[ {\dfrac{x^2}{2}}+y^2=1. \]解析由题设知 $ a^2=b^2+c^2$,${\mathrm {e}}={\dfrac{c}{a}} $.
由点 $ \left(1,{\mathrm {e}}\right) $ 在椭圆上,得\[ {\dfrac{1}{a^2}}+{\dfrac{c^2}{a^2b^2}}=1, \]解得\[ b^2=1, \]于是\[ c^2=a^2-1. \]又点 $ \left({\mathrm {e}},{\dfrac{{\sqrt{3}}}{2}} \right)$ 在椭圆上,所以\[ {\dfrac{{\mathrm {e}}^2}{a^2}}+{\dfrac{3}{4b^2}}=1, \]即\[ {\dfrac{a^2-1}{a^4}}+{\dfrac{3}{4}}=1, \]解得\[ a^2=2. \]因此,所求椭圆的方程是\[ {\dfrac{x^2}{2}}+y^2=1. \] -
设 $ A,B $ 是椭圆上位于 $ x $ 轴上方的两点,且直线 $ AF_1 $ 与直线 $ BF_2 $ 平行,$ AF_2 $ 与 $ BF_1 $ 交于点 $ P $,
(ⅰ)若 $ AF_1-BF_2={\dfrac{{\sqrt{6}}}{2}} $,求直线 $ AF_1 $ 的斜率;
(ⅱ)求证:$ PF_1+PF_2 $ 是定值.标注答案直线 $ AF_1 $ 的斜率为\[ {\dfrac{1}{m}}={\dfrac{{\sqrt{2}}}{2}}. \]解析由(1)知 $ F_1\left(-1,0\right),F_2\left(1,0\right) $,又直线 $ AF_1 $ 与 $ BF_2 $ 平行,
所以可设直线 $ AF_1 $ 的方程为\[ x+1=my, \]直线 $ BF_2 $ 的方程为\[ x-1=my. \]设 $ A\left(x_1,y_1\right),B\left(x_2,y_2\right),y_1>0,y_2>0 $.由\[ \begin{cases}{\dfrac{x^2_1}{2}}+y^2_1=1,\\x_1+1=my_1 ,\end{cases} \]得\[ \left(m^2+2\right)y^2_1-2my_1-1=0, \]解得\[ y_1={\dfrac{m+{\sqrt{2m^2+2}}}{m^2+2}}. \]故\[ \begin{split}AF_1 &={\sqrt{\left(x_1+1\right)^2+\left(y_1-0\right)^2}}\\&={\sqrt{\left(my_1\right)^2+y^2_1}}\\&={\dfrac{{\sqrt{2}}\left(m^2+1\right)+m{\sqrt{m^2+1}}}{m^2+2}}, \quad \cdots \cdots ① \end{split} \]同理,\[ BF_2={\dfrac{{\sqrt{2}}\left(m^2+1\right)-m{\sqrt{m^2+1}}}{m^2+2}}. \quad \cdots \cdots ② \](ⅰ)由 ①② 得\[ AF_1-BF_2={\dfrac{2m{\sqrt{m^2+1}}}{m^2+2}}, \]解\[ {\dfrac{2m{\sqrt{m^2+1}}}{m^2+2}}={\dfrac{{\sqrt{6}}}{2}} \]得\[ m^2=2, \]注意到 $ m>0 $,故\[ m={\sqrt{2}}.\]所以直线 $ AF_1 $ 的斜率为\[ {\dfrac{1}{m}}={\dfrac{{\sqrt{2}}}{2}}. \](ⅱ)因为直线 $ AF_1 $ 与 $ BF_2 $ 平行,所以\[ {\dfrac{PB}{PF_1}}={\dfrac{BF_2}{AF_1}}, \]于是\[ {\dfrac{PB+PF_1}{PF_1}}={\dfrac{BF_2+AF_1}{AF_1}}, \]故\[ PF_1={\dfrac{AF_1}{AF_1+BF_2}}\cdot BF_1.\]由 $ B $ 点在椭圆上知 $ BF_1+BF_2=2{\sqrt{2}} $,从而\[ PF_1={\dfrac{AF_1}{AF_1+BF_2}}\left(2{\sqrt{2}}-BF_2\right).\]同理\[ PF_2={\dfrac{BF_2}{AF_1+BF_2}}\left(2{\sqrt{2}}-AF_1\right). \]因此,\[ \begin{split} PF_1+PF_2 &={\dfrac{AF_1}{AF_1+BF_2}}\left(2{\sqrt{2}}-BF_2\right)+{\dfrac{BF_2}{AF_1+BF_2}}\left(2{\sqrt{2}}-AF_1\right)\\& =2{\sqrt{2}}-{\dfrac{2AF_1\cdot BF_2}{AF_1+BF_2}}.\end{split} \]又由 ①② 知\[AF_1+BF_2={\dfrac{2{\sqrt{2}}\left(m^2+1\right)}{m^2+2}},AF_1\cdot BF_2={\dfrac{m^2+1}{m^2+2}}.\]所以 $PF_1+PF_2={\dfrac{3{\sqrt{2}}}{2}}.$ 因此,$ PF_1+PF_2 $ 是定值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2