如图,在直角坐标系 $ xOy $ 中,点 $ P \left(1,{\dfrac{1}{2}}\right) $ 到抛物线 $ C:y^2=2px\left(p>0\right) $ 的准线的距离为 $ {\dfrac{5}{4}} $.点 $ M\left(t,1\right) $ 是 $ C $ 上的定点,$ A$,$B $ 是 $ C $ 上的两动点,且线段 $ AB $ 被直线 $ OM $ 平分.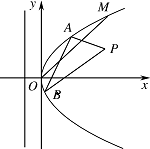

【难度】
【出处】
无
【标注】
-
求 $ p$,$t $ 的值;标注答案解析由题意知\[ \begin{cases}2pt=1,\\1+{\dfrac{p}{2}}={\dfrac{5}{4}},\end{cases} \]得\[ \begin{cases}p={\dfrac{1}{2}},\\t=1. \end{cases}\]
-
求 $ \triangle ABP $ 面积的最大值.标注答案解析设 $ A\left(x_1,y_1\right)$,$B\left(x_2,y_2\right) $,线段 $ AB $ 的中点为 $ Q\left(m,m\right) $.
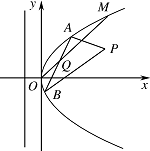 由题意知,设直线 $ AB $ 的斜率为 $ k\left(k\neq 0\right) $.
由题意知,设直线 $ AB $ 的斜率为 $ k\left(k\neq 0\right) $.
由\[ \begin{cases} y^2_1=x_1,\\y^2_2=x_2, \end{cases} \]得\[ \left(y_1-y_2\right)\left(y_1+y_2\right)=x_1-x_2, \]故\[ k\cdot 2m=1, \]所以直线 $ AB $ 方程为\[ y-m={\dfrac{1}{2m}}\left(x-m\right), \]即\[ x-2my+2m^2-m=0. \]由\[ \begin{cases}x-2my+2m^2-m=0,\\y^2=x ,\end{cases} \]消去 $ x $,整理得\[ y^2-2my+2m^2-m=0,\]所以 $\Delta =4m-4m^2>0$,即 $0<m<1$,因此\[y_1+y_2=2m,y_1\cdot y_2=2m^2-m.\]从而\[ \left|AB \right|={\sqrt{1+{\dfrac{1}{k^2}}}}\cdot |y_1-y_2|={\sqrt{1+4m^2}}\cdot {\sqrt{4m-4m^2}}.\]设点 $ P $ 到直线 $ AB $ 的距离为 $ d $.则\[ d={\dfrac{|1-2m+2m^2|}{{\sqrt{1+4m^2}}}}.\]设 $ \triangle ABP $ 的面积为 $ S $,则\[S={\dfrac{1}{2}} \left|AB \right|\cdot d= \left|1-2\left(m-m^2\right) \right|\cdot {\sqrt{m-m^2}}.\]令 $ u={\sqrt{m-m^2}},0<u\leqslant {\dfrac{1}{2}} $,则\[ S=u\left(1-2u^2\right). \]设 $ S\left(u\right)=u\left(1-2u^2\right),0<u\leqslant {\dfrac{1}{2}} $,则\[ S'\left(u\right)=1-6u^2.\]由 $S'\left(u\right)=0 $,得 $ u={\dfrac{{\sqrt{6}}}{6}}\in \left( 0,{\dfrac{1}{2}} \right) $,所以\[ S\left(u\right)_{\max}=S \left({\dfrac{{\sqrt{6}}}{6}}\right) ={\dfrac{{\sqrt{6}}}{9}}. \]故 $ \triangle ABP $ 面积的最大值为 $ {\dfrac{{\sqrt{6}}}{9}} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2