如图,设椭圆的中心为原点 $ O $,长轴在 $ x $ 轴上,上顶点为 $ A $,左、右焦点分别为 $ F_1$,$F_2 $,线段 $ OF_1$,$OF_2 $ 的中点分别为 $ B_1$,$B_2 $,且 $ \triangle {AB_1B_2 }$ 是面积为 $ 4 $ 的直角三角形.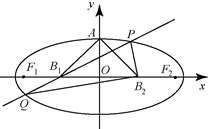

【难度】
【出处】
无
【标注】
-
求该椭圆的离心率和标准方程;标注答案解析如图,设所求椭圆的标准方程为\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left( {a > b > 0} \right),\]右焦点为 ${F_2}\left( {c,0} \right)$.因为 $\triangle A{B_1}{B_2}$ 是直角三角形,又 $\left| {A{B_1}} \right| = \left| {A{B_2}} \right|$,故 $\angle {B_1}A{B_2}$ 为直角,
因此 $\left| {OA} \right| = \left| {O{B_2}} \right|$,得 $b = \dfrac{c}{2}$.结合 ${c^2} = {a^2} - {b^2}$,得\[4{b^2} = {a^2} - {b^2},\]故\[{a^2} = 5{b^2},{c^2} = 4{b^2},\]所以离心率\[{e} = \dfrac{c}{a} = \dfrac{2}{5}\sqrt 5, \]在 $\operatorname{{\mathrm{Rt}}} \triangle A{B_1}{B_2}$ 中,$OA \perp {B_1}{B_2}$,故\[\begin{split}{S_{\triangle A{B_1}{B_2}}} &= \dfrac{1}{2} \cdot \left| {{B_1}{B_2}} \right| \cdot \left| {OA} \right| \\&= \left| {O{B_2}} \right| \cdot \left| {OA} \right| \\&= \dfrac{c}{2} \cdot b = {b^2} ,\end{split}\]由题设条件 ${S_{\triangle A{B_1}{B_2}}} = 4$,得 ${b^2} = 4$,从而\[{a^2} = 5{b^2} = 20,\]因此所求椭圆的标准方程为 $\dfrac{x^2}{20} + \dfrac{y^2}{4} = 1$. -
过 $ B_1 $ 作直线交椭圆于 $ P$,$Q $ 两点,使 $ PB_2\perp QB_2 $,求 $ \triangle PB_2Q $ 的面积.标注答案解析由(1)知 $ B_1\left(-2,0\right)$,$B_2\left(2,0\right) $.由题意知,直线 $ PQ $ 的倾斜角不为 $ 0 $,
故可设直线 $ PQ $ 的方程为 $ x=my-2 $,代入椭圆方程得\[ \left(m^2+5\right)y^2-4my-16=0. \left(*\right) \]设 $ P\left(x_1,y_1\right)$,$Q\left(x_2,y_2\right) $,则 $ y_1$,$y_2 $ 是上面方程的两根,因此\[\begin{split} y_1+y_2 &={\dfrac{4m}{m^2+5}}, y_1\cdot y_2 &=-{\dfrac{16}{m^2+5}}. \end{split}\]又\[ \begin{split}\overrightarrow {B_2P} &=\left(x_1-2,y_1\right), \overrightarrow {B_2Q} &=\left(x_2-2,y_2\right),\end{split} \]所以\[ \begin{split}\overrightarrow {B_2P}\cdot \overrightarrow {B_2Q}& =\left(x_1-2\right)\left(x_2-2\right)+y_1y_2\\&=\left(my_1-4\right)\left(my_2-4\right)+y_1y_2\\&=\left(m^2+1\right)y_1y_2-4m\left(y_1+y_2\right)+16\\&=-{\dfrac{16\left(m^2+1\right)}{m^2+5}}-{\dfrac{16m^2}{m^2+5}}+16\\&=-{\dfrac{16m^2-64}{m^2+5}}. \end{split} \]由 $ PB_2\perp QB_2 $,知 $ {\overrightarrow {B_2P}}\cdot {\overrightarrow {B_2Q}}=0$,即 $ 16m^2-64=0 $,解得 $ m=\pm 2 $,当 $ m=2 $ 时,方程 $ \left(*\right) $ 化为\[ 9y^2-8y-16=0, \]故\[ \begin{split}y_1={\dfrac{4+4{\sqrt{10}}}{9}}, y_2={\dfrac{4-4{\sqrt{10}}}{9}},|y_1-y_2|={\dfrac{8}{9}}{\sqrt{10}}, \end{split}\]$ \triangle PB_2Q $ 的面积\[ S={\dfrac{1}{2}}|B_1B_2|\cdot |y_1-y_2|={\dfrac{16}{9}}{\sqrt{10}}. \]当 $ m=-2 $ 时,同理可得(或由对称性可得)$ \triangle PB_2Q $ 的面积 $ S={\dfrac{16}{9}}{\sqrt{10}} $.
综上所述,$ \triangle PB_2Q $ 的面积为 $ {\dfrac{16}{9}}{\sqrt{10}} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2